摘要:2.设.试问:是否存在实数.使在内为减函数.且在内是增函数. 分析:根据题设条件可以求出的表达式.对于探索性问题.一般先对结论做肯定存在的假设.然后由此肯定的假设出发.结合已知条件进行推理论证.由推证结果是否出现矛盾来作出判断.解题的过程实质是一种转化的过程.由于函数是可导函数.因此选择好解题的突破口.要充分利用函数的单调性构造等价的不等式.确定适合条件的参数的取值范围.使问题获解. 解:1.由题意得. . ∴ ∴
网址:http://m.1010jiajiao.com/timu_id_4410659[举报]
设函数 ,
, (
( 为自然对数的底).
为自然对数的底).
(1)求函数 的极值;
的极值;
(2)若存在常数 和
和 ,使得函数
,使得函数 和
和 对其定义域内的任意实数
对其定义域内的任意实数 分别满足
分别满足 和
和 ,则称直线
,则称直线 :
: 为函数
为函数 和
和 的“隔离直线”.试问:函数
的“隔离直线”.试问:函数 和
和 是否存在“隔离直线”?若存在,求出“隔
是否存在“隔离直线”?若存在,求出“隔
|
查看习题详情和答案>>
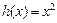 ,
,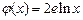 (
(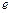 为自然对数的底).
为自然对数的底).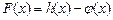 的极值;
的极值;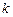 和
和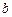 ,使得函数
,使得函数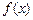 和
和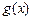 对其定义域内的任意实数
对其定义域内的任意实数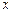 分别满足
分别满足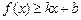 和
和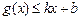 ,则称直线
,则称直线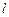 :
: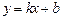 为函数
为函数 和
和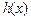 和
和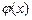 是否存在“隔离直线”?若存在,求出“隔
是否存在“隔离直线”?若存在,求出“隔 离直线”方程;若不存在,请说明理由.
离直线”方程;若不存在,请说明理由.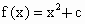 ,且
,且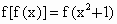 .
.