摘要:17 求 18 已知.求a 的取值范围.19. 已知递增等比数列{an}满足:a2+a3+a4=28且a3+2是a2和a4的等差中项. ⑴求数列{an}的通项公式, ⑵若.Sn=b1+b2+-+bn.求
网址:http://m.1010jiajiao.com/timu_id_4408997[举报]
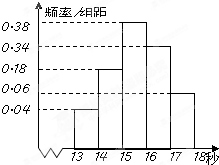 (2011•西山区模拟)为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
(2011•西山区模拟)为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.| 性别 是否 达标 |
男 | 女 | 合计 |
| 达标 | a=24 | b= 6 6 |
30 30 |
| 不达标 | c= 8 8 |
d=12 | 20 20 |
| 合计 | 32 32 |
18 18 |
n=50 |
(Ⅱ) 根据有关规定,成绩小于16秒为达标.
如果男女生使用相同的达标标准,则男女生达标情况如附表:
根据上表数据,能否有99%的把握认为“体育达标与性别有关”?若有,你能否提出一个更好的解决方法来?
附:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥K) | 0.050 | 0.010 | 0.001 |
| K | 3.841 | 6.625 | 10.828 |
调查某校100名学生的数学成绩情况,得下表:
已知从这批学生中随机抽取1名学生,抽到成绩一般的男生的概率为0.15.
(1)求x的值;
(2)若用分层抽样的方法,从这批学生中随机抽取20名,问应在优秀学生中抽多少名?
(3)已知y≥17,z≥18,优秀学生中男生不少于女生的概率.
查看习题详情和答案>>
| 一般 | 良好 | 优秀 | |
| 男生(人) | x | 18 | y |
| 女生(人) | 10 | 17 | z |
(1)求x的值;
(2)若用分层抽样的方法,从这批学生中随机抽取20名,问应在优秀学生中抽多少名?
(3)已知y≥17,z≥18,优秀学生中男生不少于女生的概率.
现有甲、乙两个项目,对甲项目每投资十万元,一年后利润是1.2万元、1.18万元、1.17万元的概率分别为
、
、
;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是P(0<P<1),设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为ζ,对乙项目每投资十万元,ξ取0、1、2时,一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量ξ1、ξ2分别表示对甲、乙两项目各投资十万元一年后的利润.
(I)求ξ1、ξ2的概率分布和数学期望Eξ1、Eξ2;
(II)当Eξ1<Eξ2时,求P的取值范围. 查看习题详情和答案>>
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
(I)求ξ1、ξ2的概率分布和数学期望Eξ1、Eξ2;
(II)当Eξ1<Eξ2时,求P的取值范围. 查看习题详情和答案>>
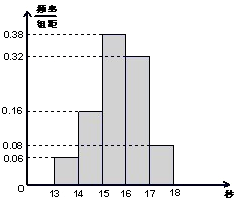 某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组;第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组;第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.(1)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(2)设m,n表示该班某两位同学的百米测试成绩,且已知m,n∈[13,14)∪[17,18],求事件“|m-n|>1”的概率. 查看习题详情和答案>>
 (2006•静安区二模)某种洗衣机在洗涤衣服时,需经过进水、清洗、排水、脱水四个连续的过程.假设进水时水量匀速增加,清洗时水量保持不变.已知进水时间为4分钟,清洗时间为12分钟,排水时间为2分钟,脱水时间为2分钟.洗衣机中的水量y(升)与时间x(分钟)之间的关系如下表所示:
(2006•静安区二模)某种洗衣机在洗涤衣服时,需经过进水、清洗、排水、脱水四个连续的过程.假设进水时水量匀速增加,清洗时水量保持不变.已知进水时间为4分钟,清洗时间为12分钟,排水时间为2分钟,脱水时间为2分钟.洗衣机中的水量y(升)与时间x(分钟)之间的关系如下表所示:| x | 0 | 2 | 4 | 16 | 16.5 | 17 | 18 | … |
| y | 0 | 20 | 40 | 40 | 29.5 | 20 | 2 | … |
(1)试写出当x∈[0,16]时y关于x的函数解析式,并画出该函数的图象;
(2)根据排水阶段的2分钟点(x,y)的分布情况,可选用y=
| a |
| x |
(3)请问(2)中求出的两个函数哪一个更接近实际情况?(写出必要的步骤)