题目内容
现有甲、乙两个项目,对甲项目每投资十万元,一年后利润是1.2万元、1.18万元、1.17万元的概率分别为| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
(I)求ξ1、ξ2的概率分布和数学期望Eξ1、Eξ2;
(II)当Eξ1<Eξ2时,求P的取值范围.
分析:(1)根据题意写出变量ξ1概率分布,表示出期望,根据条件可以看出变量ξ2符合二项分布,根据二项分布的概率写出分布列,算出期望.
(2)根据上一问做出的期望,由Eξ1<Eξ2写出概率P满足的不等关系,整理后变化为一元二次不等式的解集,采用十字相乘法得到一元二次不等式的解集,注意概率本身的限制条件.
(2)根据上一问做出的期望,由Eξ1<Eξ2写出概率P满足的不等关系,整理后变化为一元二次不等式的解集,采用十字相乘法得到一元二次不等式的解集,注意概率本身的限制条件.
解答:解:(I)由题意知ξ1概率分布为
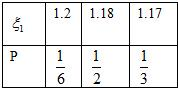
Eξ1=1.2×
+1.18×
+1.17×
=1.18.
由题设得ξ2~B(2,P),则ξ2的概率分布为
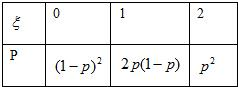
∴ξ2的数学期望为
Eξ2=1.3×(1-P)2+1.25×2P(1-P)+0.2×P2=-P2-0.1P+1.3
(II)由Eξ1<Eξ2,得:
-P2-0.1P+1.3>1.18
∴(P+0.4)(P-0.3)<0,
∴-0.4<P<0.3
∵0<p<1,
∴Eξ1<Eξ2时,p的取值范围是0<p<0.3.

Eξ1=1.2×
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
由题设得ξ2~B(2,P),则ξ2的概率分布为
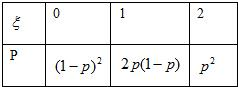
∴ξ2的数学期望为
Eξ2=1.3×(1-P)2+1.25×2P(1-P)+0.2×P2=-P2-0.1P+1.3
(II)由Eξ1<Eξ2,得:
-P2-0.1P+1.3>1.18
∴(P+0.4)(P-0.3)<0,
∴-0.4<P<0.3
∵0<p<1,
∴Eξ1<Eξ2时,p的取值范围是0<p<0.3.
点评:本小题考查二项分布、分布列、数学期望、方差等基础知识,考查同学们运用概率知识解决实际问题的能力.是一个大型的综合题,可以处在高考题目中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
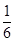 、
、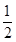 、
、 ;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是
;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是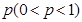 ,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为
,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为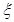 ,对乙项目投资十万元,
,对乙项目投资十万元, 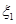 、
、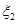 分别表示对甲、乙两项目各投资十万元一年后的利润.
分别表示对甲、乙两项目各投资十万元一年后的利润.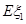 、
、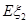 ;
;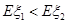 时,求
时,求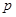 的取值范围.
的取值范围.