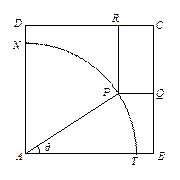摘要: 如图所示.在边长为12的正方形中.点B.C在线段AA′上.且AB=3.BC=4. 作BB1∥AA1.分别交A1A1′.AA1′于点B1.P.作CC1∥AA1.分别交A1A1′.AA1′于点C1.Q. 将该正方形沿BB1.CC1折叠.使得与AA1重合.构成如图所示的三棱柱ABC-A1B1C1. (1)在三棱柱ABC-A1B1C1中.求证:AB⊥平面BCC1B1; (2)在三棱柱ABC- A1B1C1中.求平面APQ与平面ABC所成的二面角大小. (3)在三棱柱ABC- A1B1C1中.求直线AP与直线A1Q所成角的余弦值. (4)在三棱柱ABC- A1B1C1中.求平面APQ与平面A1PQ所成的二面角大小, 湖北省天门中学2009年春季高二5月月考试卷 数学答题卡
网址:http://m.1010jiajiao.com/timu_id_4406855[举报]
(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
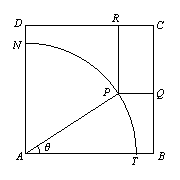
如图所示,ABCD是一块边长为7米的正方形铁皮,其中ATN是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮PQCR,其中P是![]() 上一点.设
上一点.设![]() ,长方形PQCR的面积为S平方米.
,长方形PQCR的面积为S平方米.
(1)求S关于![]() 的函数解析式;
的函数解析式;
(2)设![]() ,求S关于t的表达式以及S的最大值.
,求S关于t的表达式以及S的最大值.
 |
(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
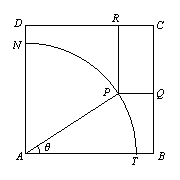
如图所示,ABCD是一块边长为7米的正方形铁皮,其中ATN是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮PQCR,其中P是![]() 上一点.设
上一点.设![]() ,长方形PQCR的面积为S平方米.
,长方形PQCR的面积为S平方米.
(1)求S关于![]() 的函数解析式;
的函数解析式;
(2)设![]() ,求S关于t的表达式以及S的最大值.
,求S关于t的表达式以及S的最大值.
 |
(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图所示,ABCD是一块边长为7米的正方形铁皮,其中ATN是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮PQCR,其中P是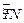
 上一点.设
上一点.设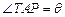 ,长方形PQCR的面积为S平方米.
,长方形PQCR的面积为S平方米.
(1)求S关于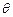 的函数解析式;
的函数解析式;
(2)设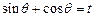 ,求S关于t的表达式以及S的最大值.
,求S关于t的表达式以及S的最大值.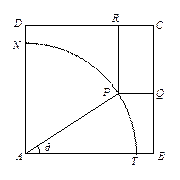
 上一点.设
上一点.设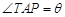 ,长方形PQCR的面积为S平方米.
,长方形PQCR的面积为S平方米.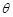 的函数解析式;
的函数解析式; 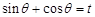 ,求S关于t的表达式以及S的最大值.
,求S关于t的表达式以及S的最大值. 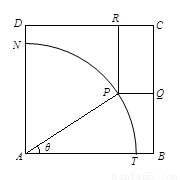
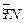
 上一点.设
上一点.设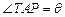 ,长方形PQCR的面积为S平方米.
,长方形PQCR的面积为S平方米.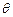 的函数解析式;
的函数解析式;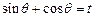 ,求S关于t的表达式以及S的最大值.
,求S关于t的表达式以及S的最大值.