摘要：44．若平面上两点..直线与线段恒有公共点.则的取值范围是 ,
网址：http://m.1010jiajiao.com/timu_id_4405994[举报]
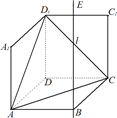如图1，在平面内，ABCD是∠BAD=60°，且AB=a的菱形，ADD′′A1和CD D′C1都是正方形．将两个正方形分别沿AD，CD折起，使D′′与D′重合于点D1．设直线l过点B且垂直于菱形ABCD所在的平面，点E是直线l上的一个动点，且与点D1位于平面ABCD同侧（图2）．（Ⅰ） 设二面角E-AC-D1的大小为θ，若
| π |
| 4 |
| π |
| 3 |
（Ⅱ）在线段D1E上存在点P，使平面PA1C1∥平面EAC，求
| D1P |
| PE |
| D1P |
| PE |
如图1，在平面内，ABCD是∠BAD=60°，且AB=a的菱形，ADD′′A1和CD D′C1都是正方形．将两个正方形分别沿AD，CD折起，使D′′与D′重合于点D1．设直线l过点B且垂直于菱形ABCD所在的平面，点E是直线l上的一个动点，且与点D1位于平面ABCD同侧（图2）．
（Ⅰ） 设二面角E-AC-D1的大小为θ，若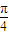
≤θ≤
，求线段BE长的取值范围；
（Ⅱ）在线段D1E上存在点P，使平面PA1C1∥平面EAC，求
与BE之间满足的关系式，并证明：当0＜BE＜a时，恒有
＜1．
查看习题详情和答案>>
（Ⅰ） 设二面角E-AC-D1的大小为θ，若
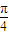≤θ≤，求线段BE长的取值范围；（Ⅱ）在线段D1E上存在点P，使平面PA1C1∥平面EAC，求
与BE之间满足的关系式，并证明：当0＜BE＜a时，恒有＜1．
查看习题详情和答案>>
(本题满分14分)
如图1，在平面内，ABCD是
的菱形，ADD``A1和CD D`C1都是正方形．将两个正方形分别沿AD，CD折起，使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面，点E是直线l上的一个动点，且与点D1位于平面ABCD同侧（图2）．
(Ⅰ) 设二面角E – AC – D1的大小为q，若
£ q £ 
，求线段BE长的取值范围；
（第20题–1）
（第20题–2）
(Ⅱ)在线段
上存在点
，使平面
平面
，求
与BE之间满足的关系式，并证明：当0 < BE < a时，恒有< 1．
的菱形，ADD``A1和CD D`C1都是正方形．将两个正方形分别沿AD，CD折起，使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面，点E是直线l上的一个动点，且与点D1位于平面ABCD同侧（图2）．
£ q £ 
，求线段BE长的取值范围；
上存在点
，使平面
平面
，求
与BE之间满足的关系式，并证明：当0 < BE < a时，恒有
的菱形，ADD``A1和CD D`C1都是正方形．将两个正方形分别沿AD，CD折起，使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面，点E是直线l上的一个动点，且与点D1位于平面ABCD同侧（图2）．
£ q £ 
，求线段BE长的取值范围；
上存在点
，使平面
平面
，求
与BE之间满足的关系式，并证明：当0 < BE < a时，恒有
