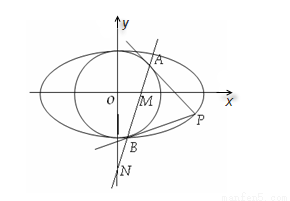
摘要:20.(注意:在试题卷上作答无效)已知椭圆和圆:.过椭圆上一点引圆的两条切线.切点分别为. 若圆过椭圆的两个焦点.求椭圆的离心率, (ⅱ)若椭圆上存在点.使得.求椭圆离心率的取值范围, (Ⅱ)设直线与轴.轴分别交于点..求证:为定值.
网址:http://m.1010jiajiao.com/timu_id_4405747[举报]
(本小题满分13分)(注意:在试题卷上作答无效)
已知函数 的反函数为
的反函数为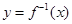 ,定义:若对给定的实数
,定义:若对给定的实数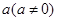 ,函数
,函数 与
与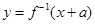 互为反函数,则称
互为反函数,则称 满足“
满足“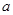 和性质”.
和性质”.
(1)判断函数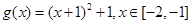 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;
(2)若 ,其中
,其中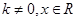 满足“2和性质”,则是否存在实数a,使得
满足“2和性质”,则是否存在实数a,使得
 对任意的
对任意的 恒成立?若存在,求出
恒成立?若存在,求出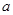 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
查看习题详情和答案>>
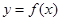 的反函数为
的反函数为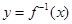 ,定义:若对给定的实数
,定义:若对给定的实数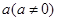 ,函数
,函数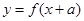 与
与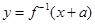 互为反函数,则称
互为反函数,则称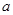 和性质”.
和性质”.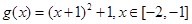 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;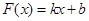 ,其中
,其中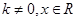 满足“2和性质”,则是否存在实数a,使得
满足“2和性质”,则是否存在实数a,使得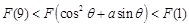 对任意的
对任意的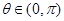 恒成立?若存在,求出
恒成立?若存在,求出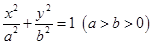 和圆
和圆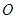 :
: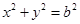 ,过椭圆上一点
,过椭圆上一点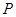 引圆
引圆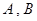 .
. 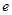 ;
; 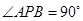 ,求椭圆离心率
,求椭圆离心率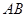 与
与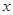 轴、
轴、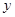 轴分别交于点
轴分别交于点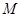 ,
,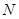 , 求证:
, 求证: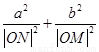 为定值.
为定值.