摘要:(1)平面向量的实际背景及基本概念 通过力和力的分析等实例.了解向量的实际背景.理解平面向量和向量相等的含义.理解向量的几何表示, (2)向量的线性运算 ①通过实例.掌握向量加.减法的运算.并理解其几何意义, ②通过实例.掌握向量数乘的运算.并理解其几何意义.以及两个向量共线的含义, ③了解向量的线性运算性质及其几何意义. (3)平面向量的基本定理及坐标表示 ①了解平面向量的基本定理及其意义, ②掌握平面向量的正交分解及其坐标表示, ③会用坐标表示平面向量的加.减与数乘运算, ④ 理解用坐标表示的平面向量共线的条件.
网址:http://m.1010jiajiao.com/timu_id_4405095[举报]
非空集合G关于运算⊕满足:(1)对任意的a,b∈G,都有a⊕b∈G,(2)存在e∈G,都有a⊕e=e⊕a=a,则称G关于运算⊕为“融洽集”.现给出下列集合和运算:
①G={非负整数},⊕为整数的加法.
②G={偶数},⊕为整数的乘法.
③G={平面向量},⊕为平面向量的加法.
④G={二次三项式},⊕为多项式的加法.
⑤G={虚数},⊕为复数的乘法.
其中G关于运算⊕为“融洽集”的是 .(写出所有“融洽集”的序号)
查看习题详情和答案>>
①G={非负整数},⊕为整数的加法.
②G={偶数},⊕为整数的乘法.
③G={平面向量},⊕为平面向量的加法.
④G={二次三项式},⊕为多项式的加法.
⑤G={虚数},⊕为复数的乘法.
其中G关于运算⊕为“融洽集”的是
 一个水平放置的平面图形,其斜二测直观图是一个等腰三角形,腰AB=AC=1,如图,则平面图形的实际面积为( )
一个水平放置的平面图形,其斜二测直观图是一个等腰三角形,腰AB=AC=1,如图,则平面图形的实际面积为( )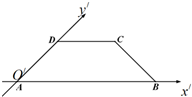 一个水平放置的平面图形,其斜二测直观图是一个等腰梯形,其底角为45°,腰和上底均为1(如图),则平面图形的实际面积为
一个水平放置的平面图形,其斜二测直观图是一个等腰梯形,其底角为45°,腰和上底均为1(如图),则平面图形的实际面积为