摘要: 解:(1)设所求反比例函数的解析式为:. 点在此反比例函数的图象上. .. 故所求反比例函数的解析式为:. (2)设直线的解析式为:. 点的反比例函数的图象上.点的纵坐标为1.设. .. 点的坐标为. 由题意.得 解得: 直线的解析式为:.
网址:http://m.1010jiajiao.com/timu_id_4404682[举报]
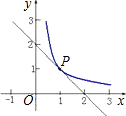 已知:如图所示,反比例函数y=
已知:如图所示,反比例函数y=| 1 |
| x |
(1)若反比例函数y=-
| k |
| x |
(2)设(1)问结论中的直线与x轴、y轴分别交于A、B两点.将∠ABO沿折痕AB翻折,设翻折后的OB边与x轴交于点C.
①直接写出点C的坐标;
②在经过A、B、C三点的抛物线的对称轴上是否存在一点P,使以P、O、M、C为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由. 查看习题详情和答案>>
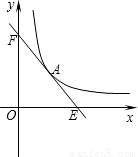
如图,已知:A(m,4)是一次函数y=kx+b与反比例函数y=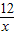 的公共点
的公共点
(1)求m的值;
(2)若该一次函数分别与x轴y轴交于E、F两点,且直角△EOF的外心为点A,试求它的解析式;
(3)在y=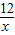 的图象上另取一点B,作BK⊥x轴于K,将(2)中的一次函数图象绕点A旋转后所得的直线记为l,设l与y轴交于点M,且4MO=FO.若在y轴上存在点P,恰好使得△PMA和△BOK的面积相等,试求点P的坐标?
的图象上另取一点B,作BK⊥x轴于K,将(2)中的一次函数图象绕点A旋转后所得的直线记为l,设l与y轴交于点M,且4MO=FO.若在y轴上存在点P,恰好使得△PMA和△BOK的面积相等,试求点P的坐标?
 查看习题详情和答案>>
查看习题详情和答案>>
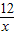 的公共点
的公共点(1)求m的值;
(2)若该一次函数分别与x轴y轴交于E、F两点,且直角△EOF的外心为点A,试求它的解析式;
(3)在y=
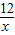 的图象上另取一点B,作BK⊥x轴于K,将(2)中的一次函数图象绕点A旋转后所得的直线记为l,设l与y轴交于点M,且4MO=FO.若在y轴上存在点P,恰好使得△PMA和△BOK的面积相等,试求点P的坐标?
的图象上另取一点B,作BK⊥x轴于K,将(2)中的一次函数图象绕点A旋转后所得的直线记为l,设l与y轴交于点M,且4MO=FO.若在y轴上存在点P,恰好使得△PMA和△BOK的面积相等,试求点P的坐标? 查看习题详情和答案>>
查看习题详情和答案>>
设![]() 是任意两个不等实数,我们规定:满足不等式
是任意两个不等实数,我们规定:满足不等式![]() 的实数
的实数![]() 的所有取值的全体叫做闭区间,表示为
的所有取值的全体叫做闭区间,表示为![]() .对于一个函数,如果它的自变量
.对于一个函数,如果它的自变量![]() 与函数值
与函数值![]() 满足:当
满足:当![]() 时,有
时,有![]() ,我们就
,我们就![]() 称此函数是闭区间
称此函数是闭区间![]() 上的“闭函数”.
上的“闭函数”.
(1)反比例函数![]() 是闭区间
是闭区间![]() 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求此函数的解析式;
上的“闭函数”,求此函数的解析式;
(3)若二次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求实数
上的“闭函数”,求实数![]() 的值.
的值.
 已知:如图所示,反比例函数y=
已知:如图所示,反比例函数y= 与直线y=-x+2只有一个公共点P,则称P为切点.
与直线y=-x+2只有一个公共点P,则称P为切点.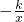 与直线y=kx+6只有一个公共点M,求当k<0时两个函数的解析式和切点M的坐标;
与直线y=kx+6只有一个公共点M,求当k<0时两个函数的解析式和切点M的坐标;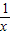 与直线y=-x+2只有一个公共点P,则称P为切点.
与直线y=-x+2只有一个公共点P,则称P为切点.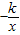 与直线y=kx+6只有一个公共点M,求当k<0时两个函数的解析式和切点M的坐标;
与直线y=kx+6只有一个公共点M,求当k<0时两个函数的解析式和切点M的坐标;