摘要:1.平面向量的数量积 ①通过物理中"功"等实例.理解平面向量数量积的含义及其物理意义, ②体会平面向量的数量积与向量投影的关系, ③掌握数量积的坐标表达式.会进行平面向量数量积的运算, ④能运用数量积表示两个向量的夹角.会用数量积判断两个平面向量的垂直关系.
网址:http://m.1010jiajiao.com/timu_id_4403908[举报]
将平面向量的数量积运算与实数的乘法运算相类比,易得下列结论:
(1)
•
=
•
;
(2)(
•
)•
=
•(
•
);
(3)
•(
+
)=
•
+
•
;
(4)由
•
=
•
(
≠
)可得
=
.
以上通过类比得到的结论正确的有( )
(1)
| a |
| b |
| b |
| a |
(2)(
| a |
| b |
| c |
| a |
| b |
| c |
(3)
| a |
| b |
| c |
| a |
| b |
| a |
| c |
(4)由
| a |
| b |
| a |
| c |
| a |
| 0 |
| b |
| c |
以上通过类比得到的结论正确的有( )
查看习题详情和答案>>
关于平面向量的数量积运算与实数的乘法运算相类比,易得下列结论:
①
•
=
•
;②(
•
)•
=
•(
•
);③
•(
+
)=
•
+
•
;
④|
•
|=|
|•|
|;⑤由
•
=
•
(
≠
),可得
=
.
以上通过类比得到的结论正确的有( )
①
| a |
| b |
| b |
| a |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| c |
④|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| c |
| a |
| 0 |
| b |
| c |
以上通过类比得到的结论正确的有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
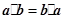 ;②
;②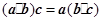 ;③
;③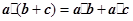 ;
;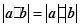 ;⑤由
;⑤由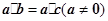 可得
可得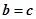 .
. ;
;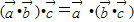 ;
;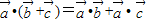 ;
; 可得
可得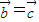 .
.