网址:http://m.1010jiajiao.com/timu_id_440321[举报]
1-5 ACADC。 6-10 ACABB 11-12 DA
13. 28 14.  15.
-4n+5 ;
15.
-4n+5 ; 16. ①③④
16. ①③④
17.(1) ,
, ,即
,即 ,
,
 ,
, ,
, ,
,  ,
,
 ,∴
,∴ . 5分
. 5分

18.解法一:证明:连结OC,

∴ .
----------------------------------------------------------------------------------1分
.
----------------------------------------------------------------------------------1分
 ,
, ,
,
∴ .
------------------------------------------------------2分
.
------------------------------------------------------2分
 在
在 中,
中,
∴ 即
即 ------------------3分
------------------3分

 面
面 . ----------------------------4分
. ----------------------------4分
(II)过O作 ,连结AE,
,连结AE,
 ,
,
∴AE在平面BCD上的射影为OE.
∴ .
.
∴  .
-----------------------------------------7分
.
-----------------------------------------7分
在 中,
中, ,
, ,
, ,
,
∴ .
.
∴二面角A-BC-D的大小为 . ---------------------------------------------------8分
. ---------------------------------------------------8分
(III)解:设点O到平面ACD的距离为
 ,
,
∴ .
.
在 中,
中, ,
,
 .
.
而 ,∴
,∴ .
.
∴点O到平面ACD的距离为 .--------------------------------12分
.--------------------------------12分
解法二:(I)同解法一.
(II)解:以O为原点,如图建立空间直角坐标系,
 则
则 
 ,
,
∴ . ------------6分
. ------------6分
设平面ABC的法向量 ,
,
 ,
, ,
,
由 .
.
设 与
与 夹角为
夹角为 ,则
,则 .
.
∴二面角A-BC-D的大小为 . --------------------8分
. --------------------8分
(III)解:设平面ACD的法向量为 ,又
,又 ,
,
 .
-----------------------------------11分
.
-----------------------------------11分
设 与
与 夹角为
夹角为 ,
,
则  - 设O 到平面ACD的距离为h,
- 设O 到平面ACD的距离为h,
∵ ,∴O到平面ACD的距离为
,∴O到平面ACD的距离为 . ---------------------12分
. ---------------------12分
19.(Ⅰ)解:设“从甲盒内取出的2个球均为黑球”为事件 ,“从乙盒内取出的2个球均为黑球”为事件
,“从乙盒内取出的2个球均为黑球”为事件 .由于事件
.由于事件 相互独立,且
相互独立,且 ,
, .
.
故取出的4个球均为黑球的概率为 .…….6分
.…….6分
(Ⅱ)解:设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件 ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件
,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件 .由于事件
.由于事件 互斥,
互斥,
且 ,
, .
.
故取出的4个球中恰有1个红球的概率为 ...12分
...12分
20. 解:(Ⅰ)由已知,当 时,
时, ……………… 2分
……………… 2分
由 ,得
,得 ,∴p=
,∴p= …………….4分
…………….4分
∴ .……………… 6分
.……………… 6分
(Ⅱ)由(1)得, . ……………… 7分
. ……………… 7分
 2 ;
①
2 ;
①
 . ② ………9分
. ② ………9分
②-①得,
= =
= . ………………12分
. ………………12分
 21.解(I)
21.解(I)


 (II)
(II)


 若
若 时,
时, 是减函数,则
是减函数,则 恒成立,得
恒成立,得


22.解(I)设

(3分)
(Ⅱ)(1)当直线 的斜率不存在时,方程为
的斜率不存在时,方程为

 …………(4分)
…………(4分)
(2)当直线 的斜率存在时,设直线的方程为
的斜率存在时,设直线的方程为 ,
,
设 ,
,
 ,得
,得
 …………(6分)
…………(6分)


 …………………8分
…………………8分
………………….9分

注意也可用 ..........12分
..........12分
| 7 |
点E是AB的中点,点P是球O的球面上任意一点,有以下判断:
(1)PE长的最大值是9;
(2)P到平面EBC的距离最大值是4+
| 7 |
(3)存在过点E的平面截球O的截面面积是3π;
(4)三棱锥P-AEC1体积的最大值是20.
其中正确判断的序号是
| 7 |
(1)PE长的最大值是9;(2)三棱锥P-EBC的最大值是
| 32 |
| 3 |
正确的是
| 7 |
(1)PE长的最大值是9;(2)三棱锥P-EBC的最大值是
| 32 |
| 3 |
正确的是______.
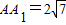 ,它的外接球的球心为O,点E是AB的中点,点P是球O的球面上任意一点,有以下判断,
,它的外接球的球心为O,点E是AB的中点,点P是球O的球面上任意一点,有以下判断, ;(3)存在过点E的平面,截球O的截面面积是3π;(4)三棱锥P-AEC1体积的最大值是20.
;(3)存在过点E的平面,截球O的截面面积是3π;(4)三棱锥P-AEC1体积的最大值是20. ,它的外接球的球心为O,点E是AB的中点,点P是球O的球面上任意一点,有以下判断,
,它的外接球的球心为O,点E是AB的中点,点P是球O的球面上任意一点,有以下判断, ;(3)存在过点E的平面,截球O的截面面积是3π;(4)三棱锥P-AEC1体积的最大值是20.
;(3)存在过点E的平面,截球O的截面面积是3π;(4)三棱锥P-AEC1体积的最大值是20.