摘要:题型1:数量积的概念 例1.判断下列各命题正确与否: (1), (2), (3)若.则, (4)若.则当且仅当时成立, (5)对任意向量都成立, (6)对任意向量.有. 解析:错,对. 点评:通过该题我们清楚了向量的数乘与数量积之间的区别于联系.重点清楚为零向量.而为零. 例2. 已知△中.过重心的直线交边于.交边于.设△的面积为.△的面积为...则(ⅰ) (ⅱ)的取值范围是 . [解析]设....因为是△的重心.故 .又..因为与共线.所以.即.又与不共线.所以及.消去.得. (ⅰ).故, (ⅱ).那么 .当与重合时..当位于中点时. .故.故但因为与不能重合.故 (2)设..是任意的非零平面向量,且相互不共线,则 ①(·)-(·)= ②||-||<|-| ③(·)-(·)不与垂直 ④(3+2)(3-2)=9||2-4||2中.是真命题的有( ) A.①② B.②③ C.③④ D.②④ 解析:(1)答案:D,因为.而,而方向与方向不一定同向. (2)答案:D①平面向量的数量积不满足结合律.故①假,②由向量的减法运算可知||.||.|-|恰为一个三角形的三条边长.由“两边之差小于第三边 .故②真,③因为[(·)-(·)]·=(·)·-(·)·=0.所以垂直.故③假,④(3+2)(3-2)=9··-4·=9||2-4||2成立.故④真. 点评:本题考查平面向量的数量积及运算律.向量的数量积运算不满足结合律. 题型2:向量的夹角 例3.(1)过△ABC的重心任作一直线分别交AB.AC于点D.E.若...则的值为( ) 2 (D)1 解析:取△ABC为正三角形易得=3.选B. 评析:本题考查向量的有关知识.如果按常规方法就比较难处理.但是用特殊值的思想就比较容易处理.考查学生灵活处理问题的能力. (2)已知向量=(cos,sin),=(cos,sin),且.那么与的夹角的大小是 . (3)已知两单位向量与的夹角为.若.试求与的夹角. (4)| |=1.| |=2.= + .且⊥.则向量与的夹角为 ( ) A.30° B.60° C.120° D.150° 解析:(2), (3)由题意..且与的夹角为. 所以.. . . 同理可得. 而. 设为与的夹角. 则. (4)C,设所求两向量的夹角为 即: 所以 点评:解决向量的夹角问题时要借助于公式.要掌握向量坐标形式的运算.向量的模的求法和向量间的乘法计算可见一斑.对于这个公式的变形应用应该做到熟练.另外向量垂直的充要条件必需掌握. 例4.(1)设平面向量..的和.如果向量...满足.且顺时针旋转后与同向.其中.则( ) A.-++= B.-+= C.+-= D.++= 已知向量与互相垂直.其中. (1)求和的值, (2)若.求的值. 解 (1)∵与互相垂直.则.即.代入得.又. ∴. (2)∵..∴. 则. 2.如图.已知△ABC中.|AC|=1,∠ABC=,∠BAC=θ,记. (1) 求关于θ的表达式; (2) 求的值域. 解:(1)由正弦定理.得 (2)由.得 ∴.即的值域为.
网址:http://m.1010jiajiao.com/timu_id_4399478[举报]
出于应用方便和数学交流的需要,我们教材定义向量的坐标如下:取
和
为直角坐标第xOy中与x轴和y轴正方向相同的单位向量,根据平面向量基本定理,对于该平面上的任意一个向量
,则存在唯一的一对实数λ,μ,使得
=λ
+μ
,我们就把实数对(λ,μ)称作向量
的坐标.并依据这样的定义研究了向量加法、减法、数乘向量及数量积的坐标运算公式.现在我们用
和
表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量,其中<
,
>=
,
(1)请你模仿直角坐标系xOy中向量坐标的定义方式,用向量
和
做基底向量定义斜坐标系x‘Oy’平面上的任意一个向量
的坐标;
(2)在(1)的基础上研究斜坐标系x‘Oy’中向量的加法、减法、数乘向量及数量积的坐标运算公式. 查看习题详情和答案>>
| e1 |
| e2 |
| a |
| a |
| e1 |
| e2 |
| a |
| i |
| j |
| i |
| j |
| π |
| 3 |
(1)请你模仿直角坐标系xOy中向量坐标的定义方式,用向量
| i |
| j |
| a |
(2)在(1)的基础上研究斜坐标系x‘Oy’中向量的加法、减法、数乘向量及数量积的坐标运算公式. 查看习题详情和答案>>
由代数式的乘法法则类比推导向量的数量积的运算法则:
①“mn=nm”类比得到“ ”;
”;
②“(m+n)t=mt+nt”类比得到“ ”;
”;
③“(m•n)t=m(n•t)”类比得到“ ”;
”;
④“t≠0,mt=xt⇒m=x”类比得到“ ”;
”;
⑤“|m•n|=|m|•|n|”类比得到“ ”;
”;
⑥“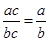 ”类比得到“
”类比得到“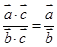 ”.
”.
以上式子中,类比得到的结论正确的个数是( )
A.1 B.2 C.3 D.4
查看习题详情和答案>>
由代数式的乘法法则类比推导向量的数量积的运算法则:
①“mn=nm”类比得到“a·b=b·a”;
②“(m+n)t=mt+nt”类比得到“(a+b)·c=a·c+b·c”;
③“(m·n)t=m(n·t)”类比得到“(a·b)·c=a·(b·c)”;
④“t≠0,mt=xt⇒m=x”类比得到“p≠0,a·p=x·p⇒a=x”;
⑤“|m·n|=|m|·|n|”类比得到“|a·b|=|a|·|b|”;
⑥“ =
= ”类比得到“
”类比得到“ =
= ”.
”.
以上的式子中,类比得到的结论正确的个数是( )
(A)1 (B)2 (C)3 (D)4
查看习题详情和答案>>
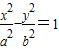 的左、右焦点,点P(x,y)是双曲线右支上的一个动点,且|PF1|的最小值为8,
的左、右焦点,点P(x,y)是双曲线右支上的一个动点,且|PF1|的最小值为8,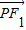 与
与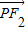 的数量积
的数量积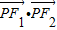 的最小值是-16.
的最小值是-16. 的左、右焦点,P为椭圆C上任意一点.
的左、右焦点,P为椭圆C上任意一点.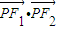 的取值范围;
的取值范围;