网址:http://m.1010jiajiao.com/timu_id_430234[举报]
| |||||||||||
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.A.选修4-1:(几何证明选讲)
如图,从O外一点P作圆O的两条切线,切点分别为A,B,
AB与OP交于点M,设CD为过点M且不过圆心O的一条弦,
求证:O,C,P,D四点共圆.
B.选修4-2:(矩阵与变换)
已知二阶矩阵M有特征值λ=3及对应的一个特征向量e1=[
1 1 |
C.选修4-4:(坐标系与参数方程)
在极坐标系中,曲线C的极坐标方程为p=2
| 2 |
| π |
| 4 |
|
D.选修4-5(不等式选讲)
已知实数x,y,z满足x+y+z=2,求2x2+3y2+z2的最小值.
若方程x2+(m-2)x-m+5=0的两个根都大于2,求实数m的取值范围.
阅读下面的解法,回答提出的问题.
解:第一步,令判别式Δ=(m-2)2-4(-m+5)≥0,
解得m≥4或m≤-4;
第二步,设两根为x1,x2,由x1>2,x2>2得
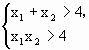 ,所以
,所以![]() .
.
所以m<-2.
第三步,由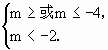 得m≤-4.
得m≤-4.
第四步,由第三步得出结论.
当m∈(-∞,-4]时,此方程两根均大于2.
但当取m=-6检验知,方程x2-8x+11=0两根为x=4±![]() ,其中4-
,其中4-![]() <2.
<2.
试问:产生错误的原因是什么?
查看习题详情和答案>>在△ABC中,a、b、c分别是角A、B、C的对边,cosB= .
.
⑴ 若cosA=- ,求cosC的值; ⑵
若AC=
,求cosC的值; ⑵
若AC= ,BC=5,求△ABC的面积.
,BC=5,求△ABC的面积.
【解析】第一问中sinB=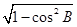 =
= , sinA=
, sinA= =
=
cosC=cos(180°-A-B)=-cos(A+B) =sinA.sinB-cosA·cosB
= ×
× -(-
-(- )×
)× =
=
第二问中,由 =
= +
+ -2AB×BC×cosB得 10=
-2AB×BC×cosB得 10= +25-8AB
+25-8AB
解得AB=5或AB=3综合得△ABC的面积为 或
或
解:⑴ sinB=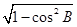 =
= , sinA=
, sinA= =
= ,………………2分
,………………2分
∴cosC=cos(180°-A-B)=-cos(A+B) ……………………3分
=sinA.sinB-cosA·cosB ……………………4分
= ×
× -(-
-(- )×
)× =
= ……………………6分
……………………6分
⑵ 由 =
= +
+ -2AB×BC×cosB得 10=
-2AB×BC×cosB得 10= +25-8AB
………………7分
+25-8AB
………………7分
解得AB=5或AB=3, ……………………9分
若AB=5,则S△ABC= AB×BC×sinB=
AB×BC×sinB= ×5×5×
×5×5× =
= ………………10分
………………10分
若AB=3,则S△ABC= AB×BC×sinB=
AB×BC×sinB= ×5×3×
×5×3× =
= ……………………11分
……………………11分
综合得△ABC的面积为 或
或
查看习题详情和答案>>
已知函数 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)设 ,若对任意
,若对任意 ,
, ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【解析】第一问利用 的定义域是
的定义域是

由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函数 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是
第二问中,若对任意 不等式
不等式 恒成立,问题等价于
恒成立,问题等价于 只需研究最值即可。
只需研究最值即可。
解: (I) 的定义域是
的定义域是 ......1分
......1分
 ............. 2分
............. 2分
由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函数 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是 ........4分
........4分
(II)若对任意 不等式
不等式 恒成立,
恒成立,
问题等价于 ,
.........5分
,
.........5分
由(I)可知,在 上,x=1是函数极小值点,这个极小值是唯一的极值点,
上,x=1是函数极小值点,这个极小值是唯一的极值点,
故也是最小值点,所以 ; ............6分
; ............6分

当b<1时, ;
;
当 时,
时, ;
;
当b>2时, ;
............8分
;
............8分
问题等价于
 ........11分
........11分
解得b<1 或 或
或  即
即 ,所以实数b的取值范围是
,所以实数b的取值范围是
查看习题详情和答案>>
