摘要:22.(1)过点P作PH⊥AC于H.则∠CPH=∠α.
网址:http://m.1010jiajiao.com/timu_id_429718[举报]
如图,在直角梯形ABCD中,AD∥BC,DC⊥BC于C,A(0,
),B(-6,0),连接BD,交y轴于点E,tan∠DBC=
(1)求直线BD的解析式;
(2)点P从B出发,以每秒1个单位的速度向终点C匀速运动,过点P作PH⊥BD于H,设HE的长为y(y≠0),点P的运动时间为t秒,求y与t的函数关系式,并直接写出t的取值范围;
(3)在(2)的条件下,连接AP,以AP为直径的圆交线段BD于Q,当tan∠APQ=
时,求t的值.

查看习题详情和答案>>
| 11 |
| 2 |
| 1 |
| 2 |
(1)求直线BD的解析式;
(2)点P从B出发,以每秒1个单位的速度向终点C匀速运动,过点P作PH⊥BD于H,设HE的长为y(y≠0),点P的运动时间为t秒,求y与t的函数关系式,并直接写出t的取值范围;
(3)在(2)的条件下,连接AP,以AP为直径的圆交线段BD于Q,当tan∠APQ=
| 1 |
| 2 |

(2011•温州一模)如图1,矩形ABCD中,AB=21,AD=12,E是CD边上的一点,DE=16,M是BC边上的中点,动点P从点A出发,沿边AB以每秒1单位长度的速度向终点B运动.设动点P的运动时间是t秒;

(1)求线段AE的长;
(2)当△ADE与△PBM相似时,求t的值;
(3)如图2,连接EP,过点P作PH⊥AE于H.
①当EP平分四边形PMEH的面积时,求t的值;
②以PE为对称轴作线段BC的轴对称图形B′C′,当线段B′C′与线段AE有公共点时,写出t的取值范围(直接写出答案).
查看习题详情和答案>>

(1)求线段AE的长;
(2)当△ADE与△PBM相似时,求t的值;
(3)如图2,连接EP,过点P作PH⊥AE于H.
①当EP平分四边形PMEH的面积时,求t的值;
②以PE为对称轴作线段BC的轴对称图形B′C′,当线段B′C′与线段AE有公共点时,写出t的取值范围(直接写出答案).
如图,菱形OABC在平面直角坐标系中,点C的坐标为(3,4),点A在x轴的正半轴上,直线AC交y轴于点D.动点P从A出发,以每秒2个单位的速度沿折线A-B-C向点C匀速运动,同时点Q从点D出发,以每秒
个单位的速度沿D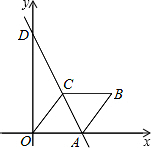 A向点A匀速运动;设点P、Q运动时间为t(秒)
A向点A匀速运动;设点P、Q运动时间为t(秒)
(1)求点A的坐标;
(2)求△PCQ的面积S(S≠0)与运动时间t的函数关系式,并写出自变量的取值范围;
(3)过点P作PH⊥AD于H,试求点P在运动的过程中t为何值时,tan∠PQH=
?
查看习题详情和答案>>
| 5 |
 A向点A匀速运动;设点P、Q运动时间为t(秒)
A向点A匀速运动;设点P、Q运动时间为t(秒)(1)求点A的坐标;
(2)求△PCQ的面积S(S≠0)与运动时间t的函数关系式,并写出自变量的取值范围;
(3)过点P作PH⊥AD于H,试求点P在运动的过程中t为何值时,tan∠PQH=
| 1 |
| 4 |

 延长交OA于F,过点P作PH⊥OC于H,连接BH、BP,设移动时间为t秒(t>0),FA=ycm,△BPH的面积为Scm2.
延长交OA于F,过点P作PH⊥OC于H,连接BH、BP,设移动时间为t秒(t>0),FA=ycm,△BPH的面积为Scm2.