Question

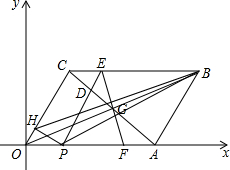
（2009•保定一模）如图，?ABCD的对角线相交于G，OC=6cm，CB=8cm，∠ABC=60°，点P从O点出发，1cm/s的速度沿OA向点A移动，D是CG的中点，连接PD并延长交CB于E，连接EG并延长交OA于F，过点P作PH⊥OC于H，连接BH、BP，设移动时间为t秒（t＞0），FA=ycm，△BPH的面积为Scm²．
（1）求y关于t的函数关系式；
（2）求S关于t的函数关系式；
（3）以O为原点，OA所在直线为x轴，建立如图所示的直角坐标系，求t=2秒时，直线BH与y轴的交点坐标．

Answer 1

分析：（1）先由题意得出OP、PA、OH的值，即可得出△CED∽△ADP，从而得出CE的值，再根据三角形全等的条件得出△CGF≌△AGF，最后得出y与t的函数关系式；
（2）根据S与三个三角形的面积之间的关系，再根据锐角三角函数即可求出S关于t的函数关系式；
（3）根据t=2秒时，求出OP和OH的值，即可求出H，B点的坐标，从而得出直线BH的解析式和直线BH与y轴的交点．

解答：解：（1）由题意得：OP=t，PA=8-t，OH=

1

2

t，
由△CED∽△ADP，得：CE=

1

3

PA=

1

3

（8-t），
而△CGE≌△AGF（ASA），
∴y=FA=CE=

1

3

（8-t），
∴y=-

1

3

t+

8

3

；

（2）S=S_△OHB+S_△OBP-S_△OHP
=

1

2

t×6×sin60°+

1

2

×

1

2

t×8×sin60°-

1

2

×

1

2

t×t×8×sin60°
=-

3

8

t²+

5 3

2

t；

（3）当t=2秒时，OP=2，OH=1，
∴H（

1

2

，

3

2

），B（11，3

3

）；
∴直线BH的解析式为y=

5 3

21

x+

8 3

21

，
∴直线BH与y轴的交点为（0，

8 3

21

）．

点评：此题考查了相似三角形的判定与性质；解题的关键是读懂题意，根据全等三角形的判定与性质以及锐角三角函数的定义进行求解即可．