摘要: 某课题学习在探讨一团周长为4a的线圈时.发现了如下两个命题:命题1:如图①.当线圈做成正三角形ABC时.能被半径为a的圆形纸片完全盖住. 命题2:如图②.当线圈做成正方形ABCD时.能被半径为a的圆形纸片完全盖住.请你继续探究下列几个问题:(1)如图③.当线圈做成正五边形ABCDE时.请说明能被半径为a的圆形纸片完全盖住,(2)如图④.当线圈做成平行四边形ABCD时.能否被半径为a的圆形纸片完全盖住?请说明理由,(3)如图⑤.当线圈做成任意形状的图形时.是否还能被半径为a的圆形纸片完全盖住?若能盖住.请通过计算说明,若不能盖住.请你说明理由.
网址:http://m.1010jiajiao.com/timu_id_429705[举报]
(本小题满分10分)
如图,在平面直角坐标系中,直线L:y=-2x-8分别与x轴、y轴相交于A、B两点,点P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P。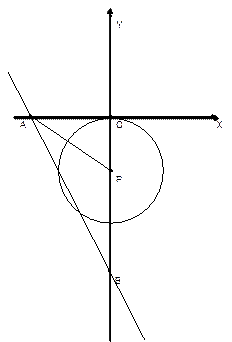
(1)连结PA,若PA=PB,试判断⊙P与X轴的位置关系,并说明理由;
(2)当K为何值时,以⊙P与直线L的两个交点和圆心P为顶点的三角形是正三角形?
(本小题满分10分)
某商场将进价40元一个的某种商品按50元一个售出时,每月能卖出500个.商场想了两个方案来增加利润:
方案一:提高价格,但这种商品每个售价涨价1元,销售量就减少10个;
方案二:售价不变,但发资料做广告。已知这种商品每月的广告费用m(千元)与销售量倍数p关系为p = ![]() ;
;
试通过计算,请你判断商场为赚得更大的利润应选择哪种方案?请说明你判断的理由!
查看习题详情和答案>>
(本小题满分10分)如图,在平面直角坐标系中,点A、B、C、P的坐标分别为(0,1)、(-1,0)、(1,0)、(-1,-1)。

【小题1】(1)求经过A、B、C三点的抛物线的表达式;
【小题2】(2)以P为位似中心,将△ABC放大,使得放大后的△A1B1C1与△OAB对应线段的比为3:1,请在右图网格中画出放大后的△A1B1C1;(所画△A1B1C1与△ABC在点P同侧);
【小题3】(3)经过A1、B1、C1三点的抛物线能否由(1)中的抛物线平移得到?请说明理由。 查看习题详情和答案>>

【小题1】(1)求经过A、B、C三点的抛物线的表达式;
【小题2】(2)以P为位似中心,将△ABC放大,使得放大后的△A1B1C1与△OAB对应线段的比为3:1,请在右图网格中画出放大后的△A1B1C1;(所画△A1B1C1与△ABC在点P同侧);
【小题3】(3)经过A1、B1、C1三点的抛物线能否由(1)中的抛物线平移得到?请说明理由。 查看习题详情和答案>>

