摘要:假设存在实数m使函数区间 上有
网址:http://m.1010jiajiao.com/timu_id_428588[举报]
(本小题满分12分)已知函数![]() 在
在![]() 处取得极值,且在点
处取得极值,且在点![]() 处的切线的斜率为2。
处的切线的斜率为2。
(1)求a、b的值; (2)求函数![]() 的单调区间和极值;
的单调区间和极值;
(3)令函数![]() ,是否存在实数m使函数
,是否存在实数m使函数![]() 在
在![]() 上的最大值比最小值大
上的最大值比最小值大![]() ?若存在,求实数m的取值范围,若不存在,说明理由。
?若存在,求实数m的取值范围,若不存在,说明理由。
(理)已知点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn),…(n∈N*)顺次为某直线l上的点,点A1(x1,0),A2(x2,0),…,An(xn,0),…顺次为x轴上的点,其中x1=a(0<a≤1).对于任意的n∈N*,△AnBnAn+1是以Bn为顶点的等腰三角形.
(1)证明xn+2-xn是常数,并求数列{xn}的通项公式.
(2)若l的方程为y=![]() ,试问在△AnBnAn+1(n∈N*)中是否存在直角三角形?若存在,求出a的值;若不存在,请说明理由.
,试问在△AnBnAn+1(n∈N*)中是否存在直角三角形?若存在,求出a的值;若不存在,请说明理由.
(文)已知函数f(x)=![]() ax3
ax3![]() x2+cx+d(a、c、d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a、c、d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
(1)求a、c、d的值.
(2)若h(x)=![]() x2-bx+
x2-bx+![]() ,解不等式f′(x)+h(x)<0.
,解不等式f′(x)+h(x)<0.
(3)是否存在实数m,使函数g(x)=f′(x)-mx在区间[m,m+2]上有最小值-5?若存在,请求出实数m的值;若不存在,请说明理由.
查看习题详情和答案>> .
. 时,求函数
时,求函数 的极值;
的极值; ,使函数
,使函数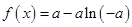 在
在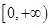 上有唯一的零点,若有,请求出
上有唯一的零点,若有,请求出 的范围;若没有,请说明理由.
的范围;若没有,请说明理由. (
( 为自然对数的底数)。
为自然对数的底数)。 ,求函数
,求函数 的单调区间;
的单调区间; ,使函数
,使函数 上是单调增函数?若存在,求出
上是单调增函数?若存在,求出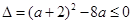
 ,又
,又 ,
,