摘要:令->0.解得:a >.
网址:http://m.1010jiajiao.com/timu_id_42776[举报]
已知函数F(x)=
ax3+bx2+cx(a≠0),F'(-1)=0.
(1)若F(x)在x=1处取得极小值-2,求函数F(x)的单调区间;
(2)令f(x)=F'(x),若f′(x)>0的解集为A,且满足A∪(0,1)=(0,+∞),求
的取值范围.
查看习题详情和答案>>
| 1 |
| 3 |
(1)若F(x)在x=1处取得极小值-2,求函数F(x)的单调区间;
(2)令f(x)=F'(x),若f′(x)>0的解集为A,且满足A∪(0,1)=(0,+∞),求
| c |
| a |
阅读材料:某同学求解sin18°的值其过程为:设α=18°,则5α=90°,从而3α=90°-2α,于是cos3α=cos(90°-2α),即cos3α=sin2α,展开得4cos3α-3cosα=2sinαcosα,∴cosα=cos18°≠0,∴4cos2α-3=2sinα,化简,得4sin2α+2sinα-1=0,解得sinα=
,∵sinα=sin18°∈(0,1),∴sinα=
(sinα=
<0舍去),即sin18°=
.试完成以下填空:设函数f(x)=ax3+1对任意x∈[-1,1]都有f(x)≥0成立,则实数a的值为
查看习题详情和答案>>
-1±
| ||
| 4 |
-1+
| ||
| 4 |
-1-
| ||
| 4 |
-1+
| ||
| 4 |
4
4
.
已知函数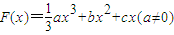 ,F'(-1)=0.
,F'(-1)=0.
(1)若F(x)在x=1处取得极小值-2,求函数F(x)的单调区间;
(2)令f(x)=F'(x),若f′(x)>0的解集为A,且满足A∪(0,1)=(0,+∞),求 的取值范围.
的取值范围.
查看习题详情和答案>>
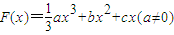 ,F'(-1)=0.
,F'(-1)=0.(1)若F(x)在x=1处取得极小值-2,求函数F(x)的单调区间;
(2)令f(x)=F'(x),若f′(x)>0的解集为A,且满足A∪(0,1)=(0,+∞),求
 的取值范围.
的取值范围.查看习题详情和答案>>
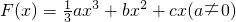 ,F'(-1)=0.
,F'(-1)=0. 的取值范围.
的取值范围.