摘要:当x ≤时:F′ 在区间上是减函数.
网址:http://m.1010jiajiao.com/timu_id_42774[举报]
在区间D上,如果函数f(x)为增函数,而函数
f(x)为减函数,则称函数f(x)为“弱增函数”.已知函数f(x)=1-
.
(1)判断函数f(x)在区间(0,1]上是否为“弱增函数”;
(2)设x1,x2∈[0,+∞),且x1≠x2,证明:|f(x2)-f(x1)|<
|x1-x2|;
(3)当x∈[0,1]时,不等式1-ax≤
≤1-bx恒成立,求实数a,b的取值范围.
查看习题详情和答案>>
| 1 |
| x |
| 1 | ||
|
(1)判断函数f(x)在区间(0,1]上是否为“弱增函数”;
(2)设x1,x2∈[0,+∞),且x1≠x2,证明:|f(x2)-f(x1)|<
| 1 |
| 2 |
(3)当x∈[0,1]时,不等式1-ax≤
| 1 | ||
|
在区间D上,如果函数f(x)为增函数,而函数 为减函数,则称函数f(x)为“弱增函数”.已知函数f(x)=1-
为减函数,则称函数f(x)为“弱增函数”.已知函数f(x)=1- .
.
(1)判断函数f(x)在区间(0,1]上是否为“弱增函数”;
(2)设x1,x2∈[0,+∞),且x1≠x2,证明:|f(x2)-f(x1)|<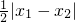 ;
;
(3)当x∈[0,1]时,不等式1-ax≤ ≤1-bx恒成立,求实数a,b的取值范围.
≤1-bx恒成立,求实数a,b的取值范围.
查看习题详情和答案>>
在区间D上,如果函数f(x)为增函数,而函数 为减函数,则称函数f(x)为“弱增函数”.已知函数f(x)=1-
为减函数,则称函数f(x)为“弱增函数”.已知函数f(x)=1-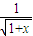 .
.
(1)判断函数f(x)在区间(0,1]上是否为“弱增函数”;
(2)设x1,x2∈[0,+∞),且x1≠x2,证明:|f(x2)-f(x1)|< ;
;
(3)当x∈[0,1]时,不等式1-ax≤ ≤1-bx恒成立,求实数a,b的取值范围.
≤1-bx恒成立,求实数a,b的取值范围.
查看习题详情和答案>>
 为减函数,则称函数f(x)为“弱增函数”.已知函数f(x)=1-
为减函数,则称函数f(x)为“弱增函数”.已知函数f(x)=1-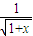 .
.(1)判断函数f(x)在区间(0,1]上是否为“弱增函数”;
(2)设x1,x2∈[0,+∞),且x1≠x2,证明:|f(x2)-f(x1)|<
 ;
;(3)当x∈[0,1]时,不等式1-ax≤
 ≤1-bx恒成立,求实数a,b的取值范围.
≤1-bx恒成立,求实数a,b的取值范围.查看习题详情和答案>>
