网址:http://m.1010jiajiao.com/timu_id_42744[举报]
(共12分,每小题4分)如图所示,一个计算装置示意图。J1、J2是数据入口,C 是计算结果的出口。计算过程是:由J1、J2 分别输入自然数m和n,经过计算所得结果由出口C输出k,即:¦(m,n)=k。此种计算装置满足以下三个性质:①¦(1,1)=1;②¦(m,n+1)=¦(m,n)+2;③¦(m+1,1)=2¦(m,1)![]()
试问:①若 J1输入5,J2输入7, 则输出结果为多少?
②若 J1输入m,J2输入自然数n, 则C输出结果为多少?
③若C输出结果为100,求:共有哪几种输入方案?

(共12分,每小题4分)如图所示,一个计算装置示意图。J1、J2是数据入口,C 是计算结果的出口。计算过程是:由J1、J2 分别输入自然数m和n,经过计算所得结果由出口C输出k,即:¦(m,n)=k。此种计算装置满足以下三个性质:①¦(1,1)=1;②¦(m,n+1)=¦(m,n)+2;③¦(m+1,1)=2¦(m,1)![]()
试问:①若 J1输入5,J2输入7, 则输出结果为多少?
②若 J1输入m,J2输入自然数n, 则C输出结果为多少?
③若C输出结果为100,求:共有哪几种输入方案?

已知函数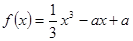
(Ⅰ)若函数 恰好有两个不同的零点,求
恰好有两个不同的零点,求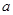 的值。
的值。
(Ⅱ)若函数 的图象与直线
的图象与直线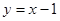 相切,求
相切,求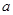 的值及相应的切点坐标。
的值及相应的切点坐标。
【解析】第一问中,利用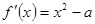
当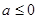 时,
时, 在
在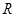 单调递增,此时
单调递增,此时 只有一个零点;
只有一个零点;
当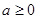 时,
时,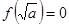 或
或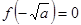 ,得
,得
第二问中,设切点为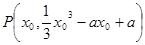 ,则
,则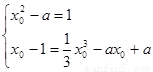
所以,当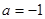 时,
时,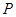 为
为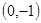 ;当
;当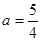 时,
时,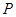 为
为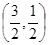
解:(Ⅰ)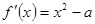 2分
2分
当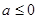 时,
时, 在
在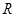 单调递增,此时
单调递增,此时 只有一个零点;
只有一个零点;
当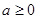 时,
时,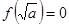 或
或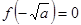 ,得
,得 4分
4分
(Ⅱ)设切点为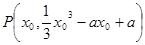 ,则
,则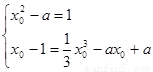 3分
3分
所以,当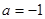 时,
时,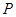 为
为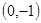 ;当
;当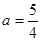 时,
时,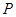 为
为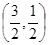
查看习题详情和答案>>
已知函数 ,
, .
.
(Ⅰ)若函数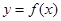 依次在
依次在 处取到极值.求
处取到极值.求 的取值范围;
的取值范围;
(Ⅱ)若存在实数 ,使对任意的
,使对任意的 ,不等式
,不等式
 恒成立.求正整数
恒成立.求正整数 的最大值.
的最大值.
【解析】第一问中利用导数在在 处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
第二问中,利用存在实数 ,使对任意的
,使对任意的 ,不等式
,不等式
 恒成立转化为
恒成立转化为 ,恒成立,分离参数法求解得到范围。
,恒成立,分离参数法求解得到范围。
解:(1)
①

(2)不等式  ,即
,即 ,即
,即 .
.
转化为存在实数 ,使对任意的
,使对任意的 ,不等式
,不等式 恒成立.
恒成立.
即不等式 在
在 上恒成立.
上恒成立.
即不等式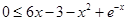 在
在 上恒成立.
上恒成立.
设 ,则.
,则.
设 ,则
,则 ,因为
,因为 ,有
,有 .
.
故 在区间
在区间 上是减函数。又
上是减函数。又
故存在 ,使得
,使得 .
.
当 时,有
时,有 ,当
,当 时,有
时,有 .
.
从而 在区间
在区间 上递增,在区间
上递增,在区间 上递减.
上递减.
又 [来源:]
[来源:]

所以当 时,恒有
时,恒有 ;当
;当 时,恒有
时,恒有
 ;
;
故使命题成立的正整数m的最大值为5
查看习题详情和答案>>
已知函数 
 R).
R).
(Ⅰ)若  ,求曲线
,求曲线
 在点
在点  处的的切线方程;
处的的切线方程;
(Ⅱ)若  对任意
对任意 
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。
第一问中,利用当 时,
时, .
.
 因为切点为(
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为:
第二问中,由题意得, 即
即 即可。
即可。
Ⅰ)当 时,
时, .
.
 ,
,
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为: . ……5分
. ……5分
(Ⅱ)解法一:由题意得, 即
即 . ……9分
. ……9分
(注:凡代入特殊值缩小范围的均给4分)
 ,
,
因为 ,所以
,所以 恒成立,
恒成立,
故 在
在 上单调递增,
……12分
上单调递增,
……12分
要使 恒成立,则
恒成立,则 ,解得
,解得 .……15分
.……15分
解法二: ……7分
……7分
(1)当 时,
时, 在
在 上恒成立,
上恒成立,
故 在
在 上单调递增,
上单调递增,
 即
即 .
……10分
.
……10分
(2)当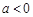 时,令
时,令 ,对称轴
,对称轴 ,
,
则 在
在 上单调递增,又
上单调递增,又
① 当 ,即
,即 时,
时, 在
在 上恒成立,
上恒成立,
所以 在
在 单调递增,
单调递增,
 即
即 ,不合题意,舍去
,不合题意,舍去
②当 时,
时, ,
不合题意,舍去 14分
,
不合题意,舍去 14分
综上所述:
查看习题详情和答案>>