摘要：由于在()内正切函数是递增函数.函数y也取最大值arctan．评述:本题主要考查复数的基本概念.三角公式和不等式等基础知识.考查综合运用所学数学知识解决问题的能力.明考复数实为三角.语言简练.情景新颖.对提高考生的数学素质要求是今后的命题方向.
网址：http://m.1010jiajiao.com/timu_id_425840[举报]
有以下五个命题
①设a＞0，f（x）=ax2+bx+c，曲线y=f（x）在点P（x，f（x））处切线的倾斜角的取值范围为[0，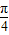
]，则点P到曲线y=f（x）对称轴距离的取值范围为[0，
]；
②一质点沿直线运动，如果由始点起经过t称后的位移为
，那么速度为零的时刻只有1秒末；
③若函数f（x）=loga（x3-ax）（a＞0，且a≠1）在区间
内单调递增，则a的取值范围是
；
④定义在R上的偶函数f（x），满足f（x+1）=-f（x），则f（x）的图象关于x=1对称；
⑤函数y=f（x-2）和y=f（2-x）的图象关于直线x=2对称．其中正确的有 ． 查看习题详情和答案>>
①设a＞0，f（x）=ax2+bx+c，曲线y=f（x）在点P（x，f（x））处切线的倾斜角的取值范围为[0，
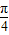]，则点P到曲线y=f（x）对称轴距离的取值范围为[0，]；②一质点沿直线运动，如果由始点起经过t称后的位移为
，那么速度为零的时刻只有1秒末；③若函数f（x）=loga（x3-ax）（a＞0，且a≠1）在区间
内单调递增，则a的取值范围是；④定义在R上的偶函数f（x），满足f（x+1）=-f（x），则f（x）的图象关于x=1对称；
⑤函数y=f（x-2）和y=f（2-x）的图象关于直线x=2对称．其中正确的有 ． 查看习题详情和答案>>
有以下五个命题
①设a＞0，f（x）=ax2+bx+c，曲线y=f（x）在点P（x0，f（x0））处切线的倾斜角的取值范围为[0，
]，则点P到曲线y=f（x）对称轴距离的取值范围为[0，
]；
②一质点沿直线运动，如果由始点起经过t称后的位移为s=
t3-
t2+2t，那么速度为零的时刻只有1秒末；
③若函数f（x）=loga（x3-ax）（a＞0，且a≠1）在区间(-
，0)内单调递增，则a的取值范围是[
，1)；
④定义在R上的偶函数f（x），满足f（x+1）=-f（x），则f（x）的图象关于x=1对称；
⑤函数y=f（x-2）和y=f（2-x）的图象关于直线x=2对称．其中正确的有 ．
查看习题详情和答案>>
①设a＞0，f（x）=ax2+bx+c，曲线y=f（x）在点P（x0，f（x0））处切线的倾斜角的取值范围为[0，
| π |
| 4 |
| 1 |
| 2a |
②一质点沿直线运动，如果由始点起经过t称后的位移为s=
| 1 |
| 3 |
| 3 |
| 2 |
③若函数f（x）=loga（x3-ax）（a＞0，且a≠1）在区间(-
| 1 |
| 2 |
| 3 |
| 4 |
④定义在R上的偶函数f（x），满足f（x+1）=-f（x），则f（x）的图象关于x=1对称；
⑤函数y=f（x-2）和y=f（2-x）的图象关于直线x=2对称．其中正确的有