题目内容
有以下五个命题①设a>0,f(x)=ax2+bx+c,曲线y=f(x)在点P(x,f(x))处切线的倾斜角的取值范围为[0,
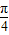 ],则点P到曲线y=f(x)对称轴距离的取值范围为[0,
],则点P到曲线y=f(x)对称轴距离的取值范围为[0, ];
];②一质点沿直线运动,如果由始点起经过t称后的位移为
 ,那么速度为零的时刻只有1秒末;
,那么速度为零的时刻只有1秒末;③若函数f(x)=loga(x3-ax)(a>0,且a≠1)在区间
 内单调递增,则a的取值范围是
内单调递增,则a的取值范围是 ;
;④定义在R上的偶函数f(x),满足f(x+1)=-f(x),则f(x)的图象关于x=1对称;
⑤函数y=f(x-2)和y=f(2-x)的图象关于直线x=2对称.其中正确的有 .
【答案】分析:对于①,f′(x)=2ax+b,因为切线的倾斜角的取值范围为[0,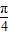 ],所以f′(x)=2ax+b∈[0,1],所以
],所以f′(x)=2ax+b∈[0,1],所以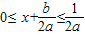 判断出①对;对于②,S′=t2-3t+2,令S′=t2-3t+2=0得x=2或x=1所以速度为零的时刻只有1秒末或2秒末,判断出②错;根据复合函数的单调性判断出③对;对于④,因为定义在R上的偶函数f(x),满足f(x+1)=-f(x),所以f(x+1)=f(-x),所以f(x)的图象关于x=1对称,判断出④对对于⑤,根据图象的平移变换判断出⑤对.
判断出①对;对于②,S′=t2-3t+2,令S′=t2-3t+2=0得x=2或x=1所以速度为零的时刻只有1秒末或2秒末,判断出②错;根据复合函数的单调性判断出③对;对于④,因为定义在R上的偶函数f(x),满足f(x+1)=-f(x),所以f(x+1)=f(-x),所以f(x)的图象关于x=1对称,判断出④对对于⑤,根据图象的平移变换判断出⑤对.
解答:解:对于①,f′(x)=2ax+b,因为切线的倾斜角的取值范围为[0,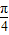 ],所以f′(x)=2ax+b∈[0,1],所以
],所以f′(x)=2ax+b∈[0,1],所以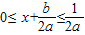 即点P到曲线y=f(x)对称轴距离的取值范围为[0,
即点P到曲线y=f(x)对称轴距离的取值范围为[0,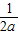 ];故①对
];故①对
对于②,S′=t2-3t+2,令S′=t2-3t+2=0得x=2或x=1所以速度为零的时刻只有1秒末或2秒末,故②错,
对于③,令t=x3-ax,因为t′=3x2-a,当a>1时,t′=3x2-a≥0在区间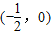 内恒成立,得a≤0不合题意;当0<a<1时t′=3x2-a≤0在区间
内恒成立,得a≤0不合题意;当0<a<1时t′=3x2-a≤0在区间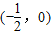 内恒成立,得a≥
内恒成立,得a≥ ,所以a的取值范围是
,所以a的取值范围是 ;所以③对;
;所以③对;
对于④,因为定义在R上的偶函数f(x),满足f(x+1)=-f(x),所以f(x+1)=f(-x),所以f(x)的图象关于x=1对称,故④对;
对于⑤,因为y=f(x)与y=f(-x)关于y轴对称,而y=f(x-2)的图象是由y=f(x)的图象向右平移2个单位;
y=f(2-x)的图象是由f(-x)的图象向有平移2个单位,所以函数y=f(x-2)和y=f(2-x)的图象关于直线x=2对称,故⑤对.
故答案为①③④⑤
点评:解决函数的图象的平移问题,一定要注意图象平移的单位是自变量x的变换的数的绝对值,然后遵循左加右减的原则.
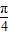 ],所以f′(x)=2ax+b∈[0,1],所以
],所以f′(x)=2ax+b∈[0,1],所以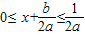 判断出①对;对于②,S′=t2-3t+2,令S′=t2-3t+2=0得x=2或x=1所以速度为零的时刻只有1秒末或2秒末,判断出②错;根据复合函数的单调性判断出③对;对于④,因为定义在R上的偶函数f(x),满足f(x+1)=-f(x),所以f(x+1)=f(-x),所以f(x)的图象关于x=1对称,判断出④对对于⑤,根据图象的平移变换判断出⑤对.
判断出①对;对于②,S′=t2-3t+2,令S′=t2-3t+2=0得x=2或x=1所以速度为零的时刻只有1秒末或2秒末,判断出②错;根据复合函数的单调性判断出③对;对于④,因为定义在R上的偶函数f(x),满足f(x+1)=-f(x),所以f(x+1)=f(-x),所以f(x)的图象关于x=1对称,判断出④对对于⑤,根据图象的平移变换判断出⑤对.解答:解:对于①,f′(x)=2ax+b,因为切线的倾斜角的取值范围为[0,
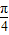 ],所以f′(x)=2ax+b∈[0,1],所以
],所以f′(x)=2ax+b∈[0,1],所以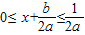 即点P到曲线y=f(x)对称轴距离的取值范围为[0,
即点P到曲线y=f(x)对称轴距离的取值范围为[0,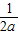 ];故①对
];故①对对于②,S′=t2-3t+2,令S′=t2-3t+2=0得x=2或x=1所以速度为零的时刻只有1秒末或2秒末,故②错,
对于③,令t=x3-ax,因为t′=3x2-a,当a>1时,t′=3x2-a≥0在区间
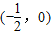 内恒成立,得a≤0不合题意;当0<a<1时t′=3x2-a≤0在区间
内恒成立,得a≤0不合题意;当0<a<1时t′=3x2-a≤0在区间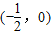 内恒成立,得a≥
内恒成立,得a≥ ,所以a的取值范围是
,所以a的取值范围是 ;所以③对;
;所以③对;对于④,因为定义在R上的偶函数f(x),满足f(x+1)=-f(x),所以f(x+1)=f(-x),所以f(x)的图象关于x=1对称,故④对;
对于⑤,因为y=f(x)与y=f(-x)关于y轴对称,而y=f(x-2)的图象是由y=f(x)的图象向右平移2个单位;
y=f(2-x)的图象是由f(-x)的图象向有平移2个单位,所以函数y=f(x-2)和y=f(2-x)的图象关于直线x=2对称,故⑤对.
故答案为①③④⑤
点评:解决函数的图象的平移问题,一定要注意图象平移的单位是自变量x的变换的数的绝对值,然后遵循左加右减的原则.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与椭圆
与椭圆 有相同的焦点;
有相同的焦点; 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率; 为常数,若
为常数,若 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线; 的焦点作直线与抛物线相交于A、B两点,则使它们的横坐标之和
的焦点作直线与抛物线相交于A、B两点,则使它们的横坐标之和 ,则动点P的
,则动点P的