网址:http://m.1010jiajiao.com/timu_id_425302[举报]
已知直三棱柱 中,
中,  ,
, ,
,
 是
是 和
和 的交点, 若
的交点, 若 .
.
(1)求 的长; (2)求点
的长; (2)求点 到平面
到平面 的距离;
的距离;
(3)求二面角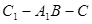 的平面角的正弦值的大小.
的平面角的正弦值的大小.

【解析】本试题主要考查了距离和角的求解运用。第一问中,利用ACC A
A 为正方形,
为正方形,  AC=3
AC=3
第二问中,利用面BB C
C C内作CD
C内作CD BC
BC ,
则CD就是点C平面A
,
则CD就是点C平面A BC
BC 的距离CD=
的距离CD= ,第三问中,利用三垂线定理作二面角的平面角,然后利用直角三角形求解得到其正弦值为
,第三问中,利用三垂线定理作二面角的平面角,然后利用直角三角形求解得到其正弦值为
解法一: (1)连AC 交A
交A C于E, 易证ACC
C于E, 易证ACC A
A 为正方形,
为正方形,  AC=3
…………… 5分
AC=3
…………… 5分
(2)在面BB C
C C内作CD
C内作CD BC
BC ,
则CD就是点C平面A
,
则CD就是点C平面A BC
BC 的距离CD=
的距离CD= … 8分
… 8分
(3) 易得AC
 面A
面A CB,
过E作EH
CB,
过E作EH A
A B于H, 连HC
B于H, 连HC ,
则HC
,
则HC
 A
A B
B

 C
C HE为二面角C
HE为二面角C -A
-A B-C的平面角. ……… 9分
B-C的平面角. ……… 9分
 sin
sin C
C HE=
HE=
 二面角C
二面角C -A
-A B-C的平面角的正弦大小为
B-C的平面角的正弦大小为 ……… 12分
……… 12分
解法二: (1)分别以直线C B、CC
B、CC 、C
、C A为x、y为轴建立空间直角坐标系, 设|CA|=h, 则C
A为x、y为轴建立空间直角坐标系, 设|CA|=h, 则C (0,
0, 0), B
(0,
0, 0), B (4,
0, 0), B(4, -3, 0), C(0, -3,
0), A
(4,
0, 0), B(4, -3, 0), C(0, -3,
0), A (0,
0, h), A(0, -3, h), G(2, -
(0,
0, h), A(0, -3, h), G(2, - , -
, - ) ……………………… 3分
) ……………………… 3分

 =(2, -
=(2, - , -
, - ),
),  =(0,
-3, -h) ……… 4分
=(0,
-3, -h) ……… 4分

 ·
· =0,
=0,
 h=3
h=3
(2)设平面A BC
BC 得法向量
得法向量 =(a, b, c),则可求得
=(a, b, c),则可求得 =(3, 4, 0) (令a=3)
=(3, 4, 0) (令a=3)
 点A到平面A
点A到平面A BC
BC 的距离为H=|
的距离为H=| |=
|= ……… 8分
……… 8分
(3) 设平面A BC的法向量为
BC的法向量为 =(x, y, z),则可求得
=(x, y, z),则可求得 =(0, 1, 1) (令z=1)
=(0, 1, 1) (令z=1)
 二面角C
二面角C -A
-A B-C的大小
B-C的大小 满足cos
满足cos =
= =
= ………
11分
………
11分
 二面角C
二面角C -A
-A B-C的平面角的正弦大小为
B-C的平面角的正弦大小为
查看习题详情和答案>>
 某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了三项测试:笔试、面试和民主评议测试,其中三人的笔试和面试成绩如下表所示:
某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了三项测试:笔试、面试和民主评议测试,其中三人的笔试和面试成绩如下表所示:| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 75 | 80 | 90 |
| 面试 | 93 | 70 | 68 |
(1)请算出三人的民主评议得分;
(2)如果根据三项测试的平均成绩录用人选,那么谁将被录用(精确到0.01)?
(3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按4:3:3的比例确定个人成绩,那么谁将被录用?
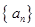 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称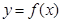 使得
使得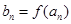 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称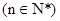 .
.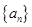 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若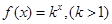 是数列
是数列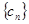 的首项为2010,
的首项为2010,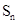 是数列
是数列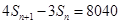 ,证明
,证明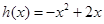 ,
,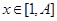 ,和数列1,
,和数列1,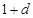 ,
,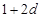 ,(
,(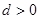 )提出一个正确的命题,并说明理由.
)提出一个正确的命题,并说明理由.