摘要:本章内容在高考中无论在题型.题量和难度方面都比较稳定.复习时应注意以下几点:(1)理解定义.定理本质.科学地进行判断与论证.依据定义.定理.对立体几何中各元素间的关系或几何体的某些特性的存在与否进行判定与论证是高考的重要内容之一.高考中常以判断题的形式出现.解此类问题.关键是相关的概念.判定.性质定理要清楚.其次要否定某些错误的判断.可运用运动变化的思想.让点或直线或平面在满足条件的情况下充分运动.往往可以发现一些特殊情况或极端位置时出现错误.另外将文字语言.符号语言.图形语言灵活准确地进行转化是解答这类题目的前提.再者举反例是解判断题的常用方法.(2)通过典型问题掌握基本解题方法高考中立体几何解答题基本题型是(Ⅰ)证明空间线面平行或垂直.(Ⅱ)求空间中线面的夹角或距离.(Ⅲ)求几何体的侧面积及体积.(Ⅰ)证明空间线面平行或垂直需注意以下几点:①由已知想性质.由求证想判定.即分析法与综合法相结合寻找证题思路.②立体几何论证题的解答中.利用题设条件的性质适当添加辅助线是解题的常用方法之一.③明确何时应用判定定理.何时应用性质定理.用定理时要先申明条件再由定理得出相应结论.④三垂线定理及其逆定理在高考题中使用的频率最高.在证明线线垂直时应优先考虑.应用时常需先认清所观察的平面及它的垂线.从而明确斜线.射影.面内直线的位置.再根据定理由已知的两直线垂直得出新的两直线垂直.另外通过计算证明线线垂直也是常用的方法之一.(Ⅱ)求空间中线面的夹角或距离需注意以下几点:①注意根据定义找出或作出所求的成角或距离.一般情况下.力求明确所求角或距离的位置.②作线面角的方法除平移外.补形也是常用的方法之一,求线面角的关键是寻找两“足 .而垂足的寻找通常用到面面垂直的性质定理.③求二面角高考中每年必考.复习时必须高度重视.二面角的平角的常用作法有三种:
网址:http://m.1010jiajiao.com/timu_id_425301[举报]
(本小题为必做题,满分12分)
甲、乙、丙三个同学一起参加某高校组织的自主招生考试,考试分笔试和面试两部分,笔试和面试均合格者将成为该高校的预录取生(可在高考中加分录取),两次考试过程相互独立.根据甲、乙、丙三个同学的平时成绩分析,甲、乙、丙三个同学能通过笔试的概率分别是0.6,0.5,0.4,能通过面试的概率分别是0.5,0.6,0.75.
(1)求甲、乙、丙三个同学中恰有一人通过笔试的概率;
(2)设经过两次考试后,能被该高校预录取的人数为![]() ,求随机变量
,求随机变量![]() 的期望
的期望![]() .
.
(1)一本书分别由1,2,3,4,5,6这些章组成,这些章之间存在着以下这些关系:学完第一章之后才能学后面的这几章,第6章只能在最后学习,第3章要在第2章学完之后才能学习,第5章要在第4章学完之后才能学习.画出这本书中各章的逻辑关系框图.
(2)有一道试题:有一个三角形,它的边长分别为6cm,8cm,10cm,请判断三角形的形状.
同学米虎的答案:
由勾股定理知,凡是直角三角形都是斜边的平方等于其他两边平方之和,这个三角形的一边的平方等于其他两边平方之和,所以,这个三角形是直角三角形.
请问:他的推理正确吗?如不正确,请写出正确的推理.
查看习题详情和答案>>
(2)有一道试题:有一个三角形,它的边长分别为6cm,8cm,10cm,请判断三角形的形状.
同学米虎的答案:
由勾股定理知,凡是直角三角形都是斜边的平方等于其他两边平方之和,这个三角形的一边的平方等于其他两边平方之和,所以,这个三角形是直角三角形.
请问:他的推理正确吗?如不正确,请写出正确的推理.
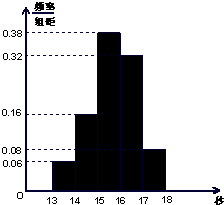 (2012•珠海二模)某学校900名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
(2012•珠海二模)某学校900名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.