摘要:根据圆柱性质.平面ABCD⊥平面ABE.AB是交线.且EH平面ABE.所以EH⊥平面ABCD.
网址:http://m.1010jiajiao.com/timu_id_425274[举报]
如图所示,圆柱的高为2,底面半径为 ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过 作圆柱的截面交下底面于
作圆柱的截面交下底面于 .
.
(1)求证: ;
;
(2)若四边形ABCD是正方形,求证 ;
;
(3)在(2)的条件下,求二面角A-BC-E的平面角的一个三角函数值。

【解析】第一问中,利用由圆柱的性质知:AD平行平面BCFE
又过 作圆柱的截面交下底面于
作圆柱的截面交下底面于 .
. ∥
∥
又AE、DF是圆柱的两条母线
 ∥DF,且AE=DF
∥DF,且AE=DF  AD∥EF
AD∥EF
第二问中,由线面垂直得到线线垂直。四边形ABCD是正方形
 又
又
BC、AE是平面ABE内两条相交直线



第三问中,设正方形ABCD的边长为x,则在
在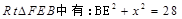

由(2)可知: 为二面角A-BC-E的平面角,所以
为二面角A-BC-E的平面角,所以
证明:(1)由圆柱的性质知:AD平行平面BCFE
又过 作圆柱的截面交下底面于
作圆柱的截面交下底面于 .
. ∥
∥
又AE、DF是圆柱的两条母线
 ∥DF,且AE=DF
∥DF,且AE=DF  AD∥EF
AD∥EF

(2) 四边形ABCD是正方形
四边形ABCD是正方形
 又
又
BC、AE是平面ABE内两条相交直线



(3)设正方形ABCD的边长为x,则在
在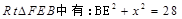

由(2)可知: 为二面角A-BC-E的平面角,所以
为二面角A-BC-E的平面角,所以
查看习题详情和答案>>
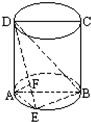 如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,AF⊥DE,F是垂足.
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,AF⊥DE,F是垂足.(1)求证:AF⊥DB;
(2)如果圆柱与三棱锥D-ABE的体积的比等于3π,求直线DE与平面ABCD所成的角. 查看习题详情和答案>>
(本小题满分12分) 如图,圆柱的轴截面AB![]() CD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的底面积与△ABE的面积之比等于π.
CD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的底面积与△ABE的面积之比等于π.
(Ⅰ)求证:AF⊥BD;
(Ⅱ)求直线DE与平面ABCD所成角的正切值.
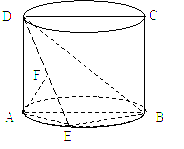
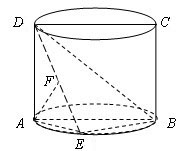
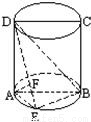 如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,AF⊥DE,F是垂足.
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,AF⊥DE,F是垂足.