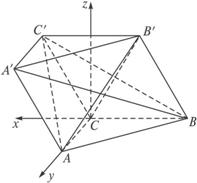
摘要:∵CB平面CA′B.∴平面CA′B⊥平面A′AB,(2)由四边形A′ABB′是菱形.∠ABB′=60°.连AB′.可知△ABB′是正三角形.取BB′的中点H.连接AH.则AH⊥BB′.又由CB⊥平面A′AB.得平面A′ABB′⊥平面C′B′BC.而AH垂直于两平面交线BB′.∴AH⊥平面C′B′BC.连结C′H.则∠AC′H为AC′与平面BCC′所成的角.
网址:http://m.1010jiajiao.com/timu_id_425263[举报]
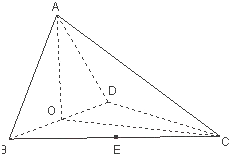 如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=
如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD= .
.
(I)求证:AO⊥平面BCD;
(II)求点E到平面ACD的距离;
(III)求二面角A-CD-B的余弦值.
查看习题详情和答案>>
如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=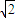 .
.
(I)求证:AO⊥平面BCD;
(II)求点E到平面ACD的距离;
(III)求二面角A-CD-B的余弦值.
 查看习题详情和答案>>
查看习题详情和答案>>
 .
.(I)求证:AO⊥平面BCD;
(II)求点E到平面ACD的距离;
(III)求二面角A-CD-B的余弦值.
 查看习题详情和答案>>
查看习题详情和答案>>
如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=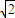 .
.
(I)求证:AO⊥平面BCD;
(II)求点E到平面ACD的距离;
(III)求二面角A-CD-B的余弦值.
 查看习题详情和答案>>
查看习题详情和答案>>
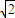 .
.(I)求证:AO⊥平面BCD;
(II)求点E到平面ACD的距离;
(III)求二面角A-CD-B的余弦值.
 查看习题详情和答案>>
查看习题详情和答案>>
 在三棱柱ABC-A′B′C′中,侧面CBB′C′⊥底面ABC,∠B′BC=60°,
在三棱柱ABC-A′B′C′中,侧面CBB′C′⊥底面ABC,∠B′BC=60°,