解:∵四棱锥S―ABCD中ABCD为直角梯形.又∵BC⊥AB ∴AD⊥AB又∵SA⊥面ABCD ∴SA⊥AB SA⊥AD又∵AD⊥AB.AD⊥SA.AB∩SA＝A∴AD⊥平面SAB——青夏教育精英家教网——

摘要：解:∵四棱锥S―ABCD中ABCD为直角梯形.又∵BC⊥AB ∴AD⊥AB又∵SA⊥面ABCD ∴SA⊥AB SA⊥AD又∵AD⊥AB.AD⊥SA.AB∩SA＝A∴AD⊥平面SAB

网址：http://m.1010jiajiao.com/timu_id_425183[举报]

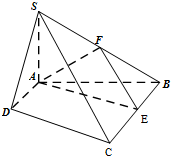如图，四棱锥S-ABCD中，SA⊥平面ABCD，底面ABCD为直角梯形，AD∥BC，∠BAD=90°，且BC=2AD=2，AB=4，SA=3．
（1）求证：平面SBC⊥平面SAB；
（2）若E、F分别为线段BC、SB上的一点（端点除外），满足

=λ．（0＜λ＜1）
①求证：对于任意的λ∈（0，1），恒有SC∥平面AEF；
②是否存在λ，使得△AEF为直角三角形，若存在，求出所有符合条件的λ值；若不存在，说明理由．

查看习题详情和答案>>

如图，在四棱锥S-ABCD中，平面SAD⊥平面ABCD．底面ABCD为矩形，AD=

a，SA=SD=a．
（Ⅰ）求证：CD⊥SA；
（Ⅱ）求二面角C-SA-D的大小．

查看习题详情和答案>>

（2008•湖北模拟）如图，已知四棱锥S-ABCD中，△SAD是边长为a的正三角形，平面SAD⊥平面ABCD，四边形ABCD为菱形，∠DAB=60°，P为AD的中点，Q为SB的中点．
（Ⅰ）求证：PQ∥平面SCD；
（Ⅱ）求二面角B-PC-Q的大小．

查看习题详情和答案>>

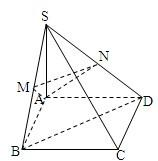17、如图，四棱锥S?ABCD中，底面ABCD是正方形，SA⊥面ABCD，且SA=AB，M、N分别为SB、SD中点，求证：
（1）DB∥平面AMN．
（2）SC⊥平面AMN．

查看习题详情和答案>>

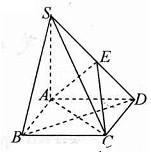如图，在底面是菱形的四棱锥S-ABCD中，SA=AB=2，SB=SD=2

．
（1）证明：BD⊥平面SAC；
（2）问：侧棱SD上是否存在点E，使得SB∥平面ACE？请证明你的结论．查看习题详情和答案>>