摘要：解析:如图9―63.取AB的中点M.连SM.OM.则SM⊥AB.OM⊥AB.又OM⊥OS.所以OM是AB与圆锥的轴的距离.OM＝1.SM＝.SO＝.AO＝.
网址：http://m.1010jiajiao.com/timu_id_425097[举报]
甲 乙两个玩一转盘游戏（转盘如图1“C为弧AB的中点”）指针指向圆弧AC时甲胜，指向圆弧BC时乙胜．后来转盘损坏如图2，甲提议连AD取AD中点E 若指针指向线段AE甲胜 指向线段ED乙胜．然后继续游戏，你觉得此时游戏还有公平性吗？
查看习题详情和答案>>
不公平
不公平
，因为p（甲）＜（不给中间分）
＜（不给中间分）
p（乙）（填＜，＞，=）
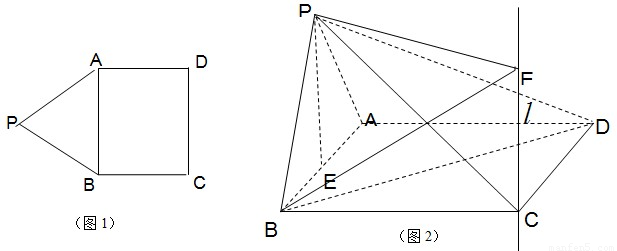
如图1，在平面内，ABCD是AB=2，BC=
的矩形，△PAB是正三角形，将△PAB沿AB折起，使PC⊥BD，如图2，E为AB的中点，设直线l过点C且垂直于矩形ABCD所在平面，点F是直线l上的一个动点，且与点P位于平面ABCD的同侧．
（1）求证：PE⊥平面ABCD；
（2）设二面角F-PB-D的平面角为θ，若θ≥45°，求线段CF长的取值范围．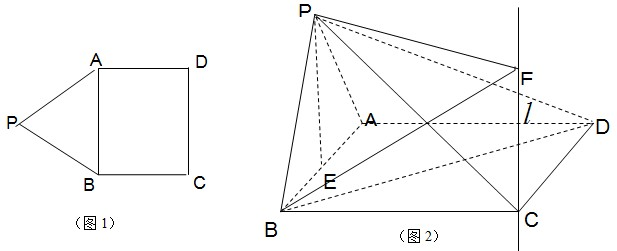
查看习题详情和答案>>
| 2 |
（1）求证：PE⊥平面ABCD；
（2）设二面角F-PB-D的平面角为θ，若θ≥45°，求线段CF长的取值范围．
查看习题详情和答案>>
如图1，在平面内，ABCD是AB=2，BC=
的矩形，△PAB是正三角形，将△PAB沿AB折起，使PC⊥BD，如图2，E为AB的中点，设直线l过点C且垂直于矩形ABCD所在平面，点F是直线l上的一个动点，且与点P位于平面ABCD的同侧．
（1）求证：PE⊥平面ABCD；
（2）设直线PF与平面PAB所成的角为θ，若45°＜θ≤60°，求线段CF长的取值范围．
查看习题详情和答案>>
| 2 |
（1）求证：PE⊥平面ABCD；
（2）设直线PF与平面PAB所成的角为θ，若45°＜θ≤60°，求线段CF长的取值范围．
查看习题详情和答案>>
的矩形，△PAB是正三角形，将△PAB沿AB折起，使PC⊥BD，如图2，E为AB的中点，设直线l过点C且垂直于矩形ABCD所在平面，点F是直线l上的一个动点，且与点P位于平面ABCD的同侧．
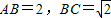的矩形，△PAB是正三角形，将△PAB沿AB折起，使PC⊥BD，如图2，E为AB的中点，设直线l过点C且垂直于矩形ABCD所在平面，点F是直线l上的一个动点，且与点P位于平面ABCD的同侧．