摘要：解析:A中直线l⊥β.lα.所以α⊥β.A为真命题.B中.在α内取两相交直线.则此二直线平行于β.则α∥β.B为真命题.D为两平面平行的性质.为真命题.C为假命题.l只有在垂直交线时才有l⊥β.否则l不垂直β.故选C.评述:本题考查平面与平面垂直.直线与平面平行的判定和性质.
网址：http://m.1010jiajiao.com/timu_id_424980[举报]
（理）设斜率为k1的直线L交椭圆C：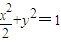
于A、B两点，点M为弦AB的中点，直线OM的斜率为k2（其中O为坐标原点，假设k1、k2都存在）．
（1）求k1?k2的值．
（2）把上述椭圆C一般化为
（a＞b＞0），其它条件不变，试猜想k1与k2关系（不需要证明）．请你给出在双曲线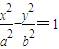
（a＞0，b＞0）中相类似的结论，并证明你的结论．
（3）分析（2）中的探究结果，并作出进一步概括，使上述结果都是你所概括命题的特例．
如果概括后的命题中的直线L过原点，P为概括后命题中曲线上一动点，借助直线L及动点P，请你提出一个有意义的数学问题，并予以解决．
查看习题详情和答案>>
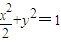于A、B两点，点M为弦AB的中点，直线OM的斜率为k2（其中O为坐标原点，假设k1、k2都存在）．（1）求k1?k2的值．
（2）把上述椭圆C一般化为
（a＞b＞0），其它条件不变，试猜想k1与k2关系（不需要证明）．请你给出在双曲线
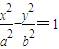（a＞0，b＞0）中相类似的结论，并证明你的结论．（3）分析（2）中的探究结果，并作出进一步概括，使上述结果都是你所概括命题的特例．
如果概括后的命题中的直线L过原点，P为概括后命题中曲线上一动点，借助直线L及动点P，请你提出一个有意义的数学问题，并予以解决．
查看习题详情和答案>>
在股票市场上，投资者常参考股价(每一股的价格)的某条平滑均线(记作MA)的变化情况来决定买入或卖出股票．股民老张在研究股票的走势图时，发现一只股票的MA均线近期走得很有特点：如果按如下图所示的方式建立平面直角坐标系xOy，则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+ψ)+b(0＜ω＜π)来描述，从C点走到今天的D点，是震荡筑底阶段，而今天出现了明显的筑底结束的标志，且D点和C点正好关于直线l：x=34对称．老张预计这只股票未来的走势如图中虚线所示，这里DE段与ABC段关于直线l对称，EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F。现在老张决定取点A(0，22)，点B(12，19)，点D(44，16)来确定解析式中的常数a、b、ω、ψ，并且已经求得
，
(1)请你帮老张算出a、b、ψ，并回答股价什么时候见顶(即求F点的横坐标)；
(2)老张如能在今天以D点处的价格买入该股票5 000股，到见顶处F点的价格全部卖出，不计其它费用，这次操作他能赚多少元？
， (1)请你帮老张算出a、b、ψ，并回答股价什么时候见顶(即求F点的横坐标)；
(2)老张如能在今天以D点处的价格买入该股票5 000股，到见顶处F点的价格全部卖出，不计其它费用，这次操作他能赚多少元？
在股票市场上，投资者常参考股价（每一股的价格）的某条平滑均线（记作MA）的变化情况来决定买入或卖出股票。股民老王在研究股票的走势图时，发现一只股票的MA均线近期走得很有特点：如果按如图所示的方式建立平面直角坐标系xoy，则股价y（元）和时间x的关系在ABC段可近似地用解析式y=asin（2x+ψ）（0＜ψ＜π）来描述，从C点走到今天的D点，是震荡筑底阶段，而今天出现了明显的筑底结束的标志，且D点和C点正好关于直线l：x=34对称。老王预计这只股票未来的走势如图中虚线所示，这里DE段与ABC段关于直线l对称，EF段是股价延续DE段的趋势（规律）走到这波上升行情的最高点F。现在老王决定取点A（0，22），点B（12，19），点D（44，16）来确定解析式中的常数a，b，w，ψ，并且已经求得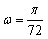
。
（1）请你帮老王算出a，b，ψ，并回答股价什么时候见顶（即求F点的横坐标）；
（2）老王如能在今天以D点处的价格买入该股票5000股，到见顶处F点的价格全部卖出，不计其它费用，这次操作他能赚多少元？
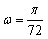。（1）请你帮老王算出a，b，ψ，并回答股价什么时候见顶（即求F点的横坐标）；
（2）老王如能在今天以D点处的价格买入该股票5000股，到见顶处F点的价格全部卖出，不计其它费用，这次操作他能赚多少元？
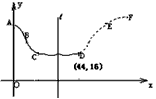
在股票市场上，投资者常参考股价（每一股的价格）的某条平滑均线（记作MA）的变化情况来决定买入或卖出股票。股民老张在研究股票的走势图时，发现一只股票的MA均线近期走得很有特点：如果按如图所示的方式建立平面直角坐标系xOy，则股价y（元）和时间x的关系在ABC段可近似地用解析式y=asin（ωx+φ）+b（0＜φ＜π）来描述，从C点走到今天的D点是震荡筑底阶段，而今天出现了明显的筑底结束的标志，且D点和C点正好关于直线l：x=34对称，老张预计这只股票未来的走势如图中虚线所示，这里DE段与ABC段关于直线l对称，EF段是股价延续DE段的趋势（规律）走到这波上升行情的最高点F。现在老张决定取点 A（0，22），点B（12，19），点D（44，16）来确定解析式中的常数a，b，ω，φ，并且已经求得
。
。
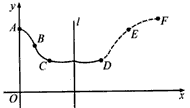
（1）请你帮老张算出a，b，φ，并回答股价什么时候见顶（即求F点的横坐标）；
（2）老张若能在今天以D点处的价格买入该股票5000股，以见顶处F点的价格全部卖出，不计其他费用，这次操作他能赚多少元？
查看习题详情和答案>>
（2）老张若能在今天以D点处的价格买入该股票5000股，以见顶处F点的价格全部卖出，不计其他费用，这次操作他能赚多少元？
已知中心在原点O，焦点F1、F2在x轴上的椭圆E经过点C（2，2），且抛物线
的焦点为F1.
（Ⅰ）求椭圆E的方程；
（Ⅱ）垂直于OC的直线l与椭圆E交于A、B两点，当以AB为直径的圆P与y轴相切时，求直线l的方程和圆P的方程.
【解析】本试题主要考查了椭圆的方程的求解以及直线与椭圆的位置关系的运用。第一问中，设出椭圆的方程，然后结合抛物线的焦点坐标得到
，又因为
，这样可知得到
。第二问中设直线l的方程为y=-x+m与椭圆联立方程组可以得到
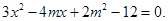，再利用
可以结合韦达定理求解得到m的值和圆p的方程。
解：(Ⅰ)设椭圆E的方程为
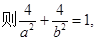①………………………………1分
②………………２分
③ 由①、②、③得a2=12,b2=6…………3分
所以椭圆E的方程为…………………………4分
(Ⅱ)依题意，直线OC斜率为1，由此设直线l的方程为y=-x+m，……………5分
代入椭圆E方程，得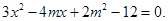…………………………6分
………………………7分
、
………………8分
………………………9分
……………………………10分
当m=3时，直线l方程为y=-x+3，此时，x1 +x2=4，圆心为（2，1），半径为2，
圆P的方程为（x-2）2+(y-1)2=4；………………………………11分
同理，当m=－3时，直线l方程为y=-x－3，
圆P的方程为（x+2）2+(y+1)2=4
查看习题详情和答案>>