网址:http://m.1010jiajiao.com/timu_id_422543[举报]
-1±
| ||
| 4 |
-1+
| ||
| 4 |
-1-
| ||
| 4 |
-1+
| ||
| 4 |
-1±
| ||
| 4 |
-1+
| ||
| 4 |
-1-
| ||
| 4 |
-1+
| ||
| 4 |
求圆心在直线y=-2x上,并且经过点A(2,-1),与直线x+y=1相切的圆的方程.
【解析】利用圆心和半径表示圆的方程,首先
设圆心为S,则KSA=1,∴SA的方程为:y+1=x-2,即y=x-3, ………4分
和y=-2x联立解得x=1,y=-2,即圆心(1,-2)
∴r=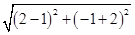 =
=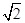 ,
,
故所求圆的方程为: +
+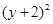 =2
=2
解:法一:
设圆心为S,则KSA=1,∴SA的方程为:y+1=x-2,即y=x-3, ………4分
和y=-2x联立解得x=1,y=-2,即圆心(1,-2) ……………………8分
∴r=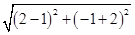 =
=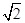 ,
………………………10分
,
………………………10分
故所求圆的方程为: +
+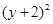 =2
………………………12分
=2
………………………12分
法二:由条件设所求圆的方程为: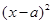 +
+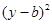 =
=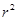
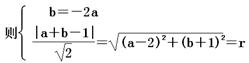 , ………………………6分
, ………………………6分
解得a=1,b=-2, 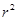 =2
………………………10分
=2
………………………10分
所求圆的方程为: +
+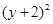 =2
………………………12分
=2
………………………12分
其它方法相应给分
查看习题详情和答案>>
在△ABC中,a、b、c分别是角A、B、C的对边,cosB= .
.
⑴ 若cosA=- ,求cosC的值; ⑵
若AC=
,求cosC的值; ⑵
若AC= ,BC=5,求△ABC的面积.
,BC=5,求△ABC的面积.
【解析】第一问中sinB= =
= , sinA=
, sinA= =
=
cosC=cos(180°-A-B)=-cos(A+B) =sinA.sinB-cosA·cosB
= ×
× -(-
-(- )×
)× =
=
第二问中,由 =
=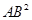 +
+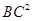 -2AB×BC×cosB得 10=
-2AB×BC×cosB得 10=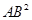 +25-8AB
+25-8AB
解得AB=5或AB=3综合得△ABC的面积为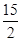 或
或
解:⑴ sinB= =
= , sinA=
, sinA= =
= ,………………2分
,………………2分
∴cosC=cos(180°-A-B)=-cos(A+B) ……………………3分
=sinA.sinB-cosA·cosB ……………………4分
= ×
× -(-
-(- )×
)× =
= ……………………6分
……………………6分
⑵ 由 =
=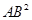 +
+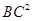 -2AB×BC×cosB得 10=
-2AB×BC×cosB得 10=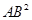 +25-8AB
………………7分
+25-8AB
………………7分
解得AB=5或AB=3, ……………………9分
若AB=5,则S△ABC= AB×BC×sinB=
AB×BC×sinB= ×5×5×
×5×5× =
=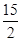 ………………10分
………………10分
若AB=3,则S△ABC= AB×BC×sinB=
AB×BC×sinB= ×5×3×
×5×3× =
= ……………………11分
……………………11分
综合得△ABC的面积为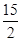 或
或
查看习题详情和答案>>