摘要:所以(a1+a2+-+an)=.评述:本题主要考查数列.数列极限.平面几何.三角函数等基本知识.考查逻辑思维能力与解决问题的能力.
网址:http://m.1010jiajiao.com/timu_id_422491[举报]
先阅读下列不等式的证法,再解决后面的问题:
已知a1,a2∈R,a1+a2=1,求证a12+a22≥
,
证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2x+a12+a22
因为对一切x∈R,恒有f(x)≥0,所以△=4-8(a12+a22)≤0,从而得a12+a22≥
,
(1)若a1,a2,…,an∈R,a1+a2+…+an=1,请写出上述结论的推广式;
(2)参考上述解法,对你推广的结论加以证明. 查看习题详情和答案>>
已知a1,a2∈R,a1+a2=1,求证a12+a22≥
| 1 |
| 2 |
证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2x+a12+a22
因为对一切x∈R,恒有f(x)≥0,所以△=4-8(a12+a22)≤0,从而得a12+a22≥
| 1 |
| 2 |
(1)若a1,a2,…,an∈R,a1+a2+…+an=1,请写出上述结论的推广式;
(2)参考上述解法,对你推广的结论加以证明. 查看习题详情和答案>>
请阅读下列材料:
若两个实数a1,a2满足a1+a2=1,则
+
≥
证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2x+a12+a22,因为对一切实数x,f(x)≥O恒成立,所以△=4-4×2(a12+a22)≤0,即
+
≥
根据上述证明方法,若n个实数a1,a2,…,an满足a1+a2+…+an=1时,你能得到的不等式为: .
查看习题详情和答案>>
若两个实数a1,a2满足a1+a2=1,则
| a | 2 1 |
| a | 2 2 |
| 1. |
| 2 |
| a | 2 1 |
| a | •2 2 |
| 1 |
| 2 |
用n个不同的实数a1,a2,…,an可得到n!个不同的排列,每个排列为一行写成一个n!行的数阵.对第i行ai1,ai2,…,ain,记bi=-ai1+2ai2-3ai3+…+(-1)nnam,i=1,2,3,…,n!.例如:用1,2,3可得数阵如下图,由于此数阵中每一列各数之和都是12,所以,b1+b2+…+b6=-12+2×12-3×12=-24,那么,在用1,2,3,4,5形成的数阵中,b1+b2+…+b120等于( )

A.-3 600 B.1 800 C.-1 080 D.-720
查看习题详情和答案>>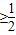 ,
,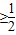 ,
,