摘要:(Ⅱ)设y=f2(x)(x∈[.1])的反函数为y=g(x).a1=1.a2=g(a1).-.an=g(an-1),求数列{an}的通项公式.并求an,
网址:http://m.1010jiajiao.com/timu_id_422338[举报]
24.已知函数f(x)=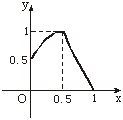
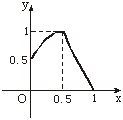
其中f1(x)=-2(x-![]() )2+1,f2(x)=-2x+2.
)2+1,f2(x)=-2x+2.
(Ⅰ)在下面坐标系上画出y=f(x)的图象;
(Ⅱ)设y=f2(x)(x![]() [
[![]() ])的反函数为y=g(x),a1=1,a2=g(a1),…,an=g(an-1);
])的反函数为y=g(x),a1=1,a2=g(a1),…,an=g(an-1);
求数列{an}的通项公式,并求![]() ;
;
(Ⅲ)若x0![]() [0,
[0,![]() ),x1=f(x0),f(x1)=x0,求x0.
),x1=f(x0),f(x1)=x0,求x0.
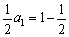
设y=f(x)为定义在区间I上的函数,若对I上任意两个实数x1,x2都有f(
)≤
[f(x1)+f(x2)]成立,则f(x)称为I上的凹函数.
(1)判断f(x)=
(x>0)是否为凹函数?
(2)已知函数f2(x)=x|ax-3|(a≠0)为区间[3,6]上的凹函数,请直接写出实数a的取值范围(不要求写出解题过程);
(3)设定义在R上的函数f3(x)满足对于任意实数x,y都有f3(x+y)=f3(x)•f3(y).求证:f3(x)为R上的凹函数.
查看习题详情和答案>>
| x1+x2 |
| 2 |
| 1 |
| 2 |
(1)判断f(x)=
| 3 |
| x |
(2)已知函数f2(x)=x|ax-3|(a≠0)为区间[3,6]上的凹函数,请直接写出实数a的取值范围(不要求写出解题过程);
(3)设定义在R上的函数f3(x)满足对于任意实数x,y都有f3(x+y)=f3(x)•f3(y).求证:f3(x)为R上的凹函数.
设函数y=f(x)的定义域为R,f(1)=2,且对任意x1,x2∈R,都有f(x1+x2)=f(x1)+f(x2),当x>0时,f(x)是增函数,则函数y=-f2(x)在区间[-3,-2]上的最大值是
查看习题详情和答案>>
-16
-16
. 已知函数
已知函数