题目内容
 已知函数f(x)=
已知函数f(x)=
|
| 1 |
| 2 |
(1)如图,在下面坐标系上画出y=f(x)的图象;
(2)设y=f2(x)(x∈[
| 1 |
| 2 |
an=g(an-1),求数列{an}的通项公式,并求
| lim |
| n→∞ |
(3)若x0∈[0,
| 1 |
| 2 |
分析:(1)分别作出函数在区间[0,
),[
,1]上的图象;
(2)求出函数y=g(x)的解析式,利用递推法,及等比数列的求和公式求出an,并求其极限;
(3)x1=f1(x0)=1-2(x0-
)2∈[
,1],f2(x1)=2-2[1-2(x0-
)2]=4(x0-
)2
由f2(x1)=x0,整理得4x02-5x0+1=0,计算出x0.
| 1 |
| 2 |
| 1 |
| 2 |
(2)求出函数y=g(x)的解析式,利用递推法,及等比数列的求和公式求出an,并求其极限;
(3)x1=f1(x0)=1-2(x0-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由f2(x1)=x0,整理得4x02-5x0+1=0,计算出x0.
解答: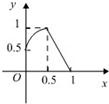 解(1)如图所示:
解(1)如图所示:
说明:图象过(0,
)、(
,1)、(1,0)点;
在区间(0,
)上的图象为上凸的曲线段;
在区间[
,1]上的图象为直线段.
(2)f2(x)=-2x-2,x∈[
,1]的反函数为:
y=1-
,x∈[0,1](5分)
由已知条件得:
a1=1
a2=1-
a1=1-
a3=1-
a2=1-
+(
)2
a4=1+(-
)1+(-
)2+(-
)3,
∴an=(-
)0+(-
)1+(-
)2++(-
)n-1=
即an=
[1-(
)n],(8分)
∴
an=
[1-(
)n]=
(10分)
(3):由已知x0∈(0,
),
∴x1=f1(x0)=1-2(x0-
)2,
由f1(x)的值域,得x1∈[
,1]
∴f2(x1)=2-2[1-2(x0-
)2]=4(x0-
)2
由f2(x1)=x0,整理得4x02-5x0+1=0,
解得x0=1,x0=
因为x0∈(0,
),所以x0=
(14分)
 解(1)如图所示:
解(1)如图所示:说明:图象过(0,
| 1 |
| 2 |
| 1 |
| 2 |
在区间(0,
| 1 |
| 2 |
在区间[
| 1 |
| 2 |
(2)f2(x)=-2x-2,x∈[
| 1 |
| 2 |
y=1-
| x |
| 2 |
由已知条件得:
a1=1
a2=1-
| 1 |
| 2 |
| 1 |
| 2 |
a3=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
a4=1+(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴an=(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
1-(-
| ||
1-(-
|
即an=
| 2 |
| 3 |
| 1 |
| 2 |
∴
| lim |
| n→∞ |
| lim |
| n→∞ |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
(3):由已知x0∈(0,
| 1 |
| 2 |
∴x1=f1(x0)=1-2(x0-
| 1 |
| 2 |
由f1(x)的值域,得x1∈[
| 1 |
| 2 |
∴f2(x1)=2-2[1-2(x0-
| 1 |
| 2 |
| 1 |
| 2 |
由f2(x1)=x0,整理得4x02-5x0+1=0,
解得x0=1,x0=
| 1 |
| 4 |
因为x0∈(0,
| 1 |
| 2 |
| 1 |
| 4 |
点评:本小题主要考查函数及数列的基本概念和性质,考查分析、归纳、推理、运算的能力.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目