摘要：(Ⅱ)方法1 由
网址：http://m.1010jiajiao.com/timu_id_418154[举报]
（Ⅰ）求证：
=
；
（Ⅱ）利用第（Ⅰ）问的结果证明Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1；
（Ⅲ）其实我们常借用构造等式，对同一个量算两次的方法来证明组合等式，譬如：（1+x）1+（1+x）2+（1+x）3+…+（1+x）n=
=
；，由左边可求得x2的系数为C22+C32+C42+…+Cn2，利用右式可得x2的系数为Cn+13，所以C22+C32+C42+…+Cn2=Cn+13．请利用此方法证明：（C2n0）2-（C2n1）2+（C2n2）2-（C2n3）2+…+（C2n2n）2=（-1）nC2nn．
查看习题详情和答案>>
| C | m n |
| n |
| m |
| C | m-1 n-1 |
（Ⅱ）利用第（Ⅰ）问的结果证明Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1；
（Ⅲ）其实我们常借用构造等式，对同一个量算两次的方法来证明组合等式，譬如：（1+x）1+（1+x）2+（1+x）3+…+（1+x）n=
| (1+x)[1-(1+x)n] |
| 1-(1+x) |
| (1+x)n+1-(1+x) |
| x |
（）某企业有3个分厂生产同一种电子产品，第一、二、三分厂的产量之比为1：2：1，用分层抽样方法（每个分厂的产品为一层）从3个分厂生产的电子产品中共取100件作使用寿命的测试，由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分别为980h，1020h，1032h，则抽取的100件产品的使用寿命的平均值为 h.
查看习题详情和答案>>
（Ⅰ）求证：
；
（Ⅱ）利用第（Ⅰ）问的结果证明Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1；
（Ⅲ）其实我们常借用构造等式，对同一个量算两次的方法来证明组合等式，譬如：（1+x）1+（1+x）2+（1+x）3+…+（1+x）n=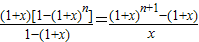
；，由左边可求得x2的系数为C22+C32+C42+…+Cn2，利用右式可得x2的系数为Cn+13，所以C22+C32+C42+…+Cn2=Cn+13．请利用此方法证明：（C2n）2-（C2n1）2+（C2n2）2-（C2n3）2+…+（C2n2n）2=（-1）nC2nn．
查看习题详情和答案>>
；（Ⅱ）利用第（Ⅰ）问的结果证明Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1；
（Ⅲ）其实我们常借用构造等式，对同一个量算两次的方法来证明组合等式，譬如：（1+x）1+（1+x）2+（1+x）3+…+（1+x）n=
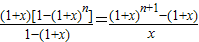；，由左边可求得x2的系数为C22+C32+C42+…+Cn2，利用右式可得x2的系数为Cn+13，所以C22+C32+C42+…+Cn2=Cn+13．请利用此方法证明：（C2n）2-（C2n1）2+（C2n2）2-（C2n3）2+…+（C2n2n）2=（-1）nC2nn．查看习题详情和答案>>
（理）若直线
|
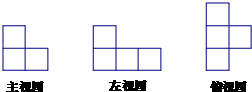
（文）由若干个棱长为1的正方体组成的几何体的三视图如图所示，则该几何体的体积为
由一组样本数据（x1，y1），（x2，y2），（x3，y3）…（xn，yn）得到的回归直线方程
=bx+a，那么，下面说法不正确的是（ ）
| ? |
| y |
A、直线
| ||||||||||||||||||
B、直线
| ||||||||||||||||||
C、直线
| ||||||||||||||||||
D、直线
|
