摘要：∵ΔPAQ为等腰直角三角形.∴又∵ΔPAF为直角三角形.
网址：http://m.1010jiajiao.com/timu_id_4171[举报]
点P（x0，y0）是曲线y=
（x＞0）上的一个动点，曲线C在点P处的切线与x，y轴分别交于A，B两点，点O是坐标原点，有下列三个命题：
①PA=PB；
②△OAB的面积是定值；
③曲线C上存在两点M，N，使得△OMN为等腰直角三角形．
其中真命题的个数是
查看习题详情和答案>>
| 1 | x |
①PA=PB；
②△OAB的面积是定值；
③曲线C上存在两点M，N，使得△OMN为等腰直角三角形．
其中真命题的个数是
2
2
（填写命题的代号）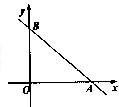
如图直线l与x轴、y轴的正半轴分别交于A、B两点，OA、OB的长分别是关于x的方程x2-14x+4（AB+2）=0的两个根（OA＜OB），P为直线l上异于A、B两点之间的一动点． 且PQ∥OB交OA于点Q．（1）求直线lAB斜率的大小；
（2）若S△PAQ=
| 1 | 3 |
（3）在y轴上是否存在点M，使△MPQ为等腰直角三角形，若存在，求出点M的坐标；
若不存在，说明理由． 查看习题详情和答案>>
（2012•海淀区二模）点P（x，y）是曲线C：y=
（x＞0）上的一个动点，曲线C在点P处的切线与x轴、y轴分别交于A，B两点，点O是坐标原点．给出三个命题：
①|PA|=|PB|；
②△OAB的周长有最小值4+2
；
③曲线C上存在两点M，N，使得△OMN为等腰直角三角形．
其中真命题的个数是（ ）
| 1 |
| x |
①|PA|=|PB|；
②△OAB的周长有最小值4+2
| 2 |
③曲线C上存在两点M，N，使得△OMN为等腰直角三角形．
其中真命题的个数是（ ）
查看习题详情和答案>>
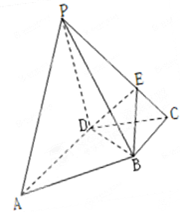如图，四棱锥P-ABCD中，AD∥BC，AD⊥DC，AD=2BC=2CD=2，侧面APD为等腰直角三角形，∠APD=90°，平面PAD⊥底面ABCD，若
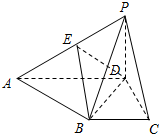（2010•宿州三模）已知四边形ABCD为直角梯形，∠ADC=90°，AD∥BC，△ABD为等腰直角三角形，平面PAD⊥平面ABCD，E为PA的中点，