网址：http://m.1010jiajiao.com/timu_id_416282[举报]
一、填空题（本大题满分60分，共12小题，每小题满分5分）
1． 
2． 
3．第四象限
4． 
5． 
6． 4 7． 
8． ―2
9． ―2或8 10．必要非充分 11． ①③④ 12． 2
二、选择题（本大题满分16分，共4小题，每小题满分4分）
13．C 14．D 15．B 16．B
三、解答题（本大题满分74，共5小题）
17．解：设正四棱柱的底边长为a
则
…………4分
18．（本题满分14分）
解：由行列式得：
…………3分
由正、余弦定理得：
…………6分
………………9分
又
………………12分
……………………14分
19．（本题满分14分）
解：设二次函数
，
二次函数
又∵m、n为正整数，
…………14分
20．（本题满分16分，第1小题满分6分，第2小题满分10分）
解：（1）
由定义得：当m=2时，M的轨迹是一条射线，方程为：
………………2分
当
时，M的轨迹是一支双曲线，方程为：
………………6分
（2）∵直线l与M点轨迹交于B、C两点，∴M的轨迹方程为：
（*）
…………9分
将m=3代入（*）式，两根异号，不符合两根均大于2
∴不存在m满足条件。 ………………16分
21．（本题满分16分，第1小题满分6分，第2小题满分10分）
解：（1）由题知：
所以
………………4分
（2）由题知：每个图形的边长都相等，且长度变为原来的
的递推公式为
（3）当由
的小等边三角形，
共有
个。
…………12分
…………16分
………………18分
本资料由《七彩教育网》www.7caiedu.cn 提供！
图中的曲线叫雪花曲线(Koch Snowflake)，它的生成方法是：
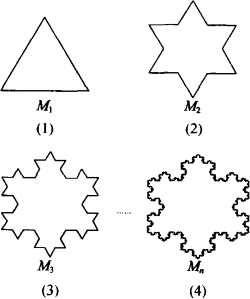
(1)将正三角形图(1)的每边三等分，并以中间的那一条线段为一底边向形外作等边三角形，然后去掉底边，得到图(2)；
(2)将图(2)的每边三等分，重复上述的作图方法，得到图(3)；
(3)再按上述方法继续做下去，就可以得到图(4)所示的曲线．
将图(1)、(2)、(3)…中的图形依次记作M1、M2、M3、…．
思考1：请分别说出M1、M2、M3的边数，想一想、如何得到M4的边数？
思考2：如果知道了Mn－1的边数，我们能否知道Mn的边数？
（i）将正三角形（图①）的每边三等分，并以中间的那一条线段为一底边向形外作等边三角形，然后去掉底边，得到图②；
（ii）将图②的每边三等分，重复上述作图方法，得到图③；
（iii）再按上述方法无限多次继续作下去，所得到的曲线就是雪花曲线．
将图①、图②、图③…中的图形依次记作M1、M2、…、Mn…设M1的边长为1．
求：（1）Mn的边数an；
（2）Mn的边长Ln；
（3）Mn的面积Sn的极限．
