题目内容
冬天,洁白的雪花飘落时十分漂亮.为研究雪花的形状,1904年,瑞典数学家科克(Koch Heige Von)把雪花理想化,得到了雪花曲线,也叫科克曲线.它的形成过程如下:
(i)将正三角形(图①)的每边三等分,并以中间的那一条线段为一底边向形外作等边三角形,然后去掉底边,得到图②;
(ii)将图②的每边三等分,重复上述作图方法,得到图③;
(iii)再按上述方法无限多次继续作下去,所得到的曲线就是雪花曲线.
将图①、图②、图③…中的图形依次记作M1、M2、…、Mn…设M1的边长为1.
求:(1)Mn的边数an;
(2)Mn的边长Ln;
(3)Mn的面积Sn的极限.
【答案】分析:(1)由题知:an递推公式为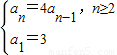 ,从而可知{an}为等比数列,故可求通项公式
,从而可知{an}为等比数列,故可求通项公式
(2)由题知:每个图形的边长都相等,且长度变为原来的 ,从而边长bn的递推公式为
,从而边长bn的递推公式为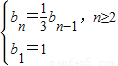 ,故可求)Mn的边数Ln;
,故可求)Mn的边数Ln;
(3)当由Mn-1生成Mn时,每条边上多了一个面积为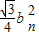 的小等边三角形,共有an-1个.从而可求Mn的面积Sn,进而可求极限.
的小等边三角形,共有an-1个.从而可求Mn的面积Sn,进而可求极限.
解答:解:(1)由题知:an递推公式为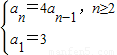
所以{an}为等比数列,其通项公式为an=3•4n-1
(2)由题知:每个图形的边长都相等,且长度变为原来的 ,
,
所以边长bn的递推公式为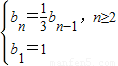
∴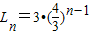
(3)当由Mn-1生成Mn时,每条边上多了一个面积为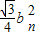 的小等边三角形,共有an-1个.
的小等边三角形,共有an-1个.
∴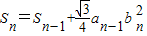
∵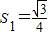
∴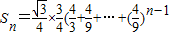
∴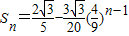
∴Mn的面积Sn的极限为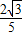
点评:本题以实际问题为载体,考查数列模型的构建,考查数列的极限,有一定的综合性.
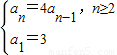 ,从而可知{an}为等比数列,故可求通项公式
,从而可知{an}为等比数列,故可求通项公式(2)由题知:每个图形的边长都相等,且长度变为原来的
 ,从而边长bn的递推公式为
,从而边长bn的递推公式为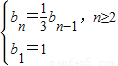 ,故可求)Mn的边数Ln;
,故可求)Mn的边数Ln;(3)当由Mn-1生成Mn时,每条边上多了一个面积为
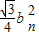 的小等边三角形,共有an-1个.从而可求Mn的面积Sn,进而可求极限.
的小等边三角形,共有an-1个.从而可求Mn的面积Sn,进而可求极限.解答:解:(1)由题知:an递推公式为
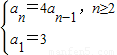
所以{an}为等比数列,其通项公式为an=3•4n-1
(2)由题知:每个图形的边长都相等,且长度变为原来的
 ,
,所以边长bn的递推公式为
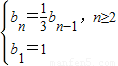
∴
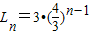
(3)当由Mn-1生成Mn时,每条边上多了一个面积为
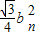 的小等边三角形,共有an-1个.
的小等边三角形,共有an-1个.∴
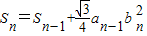
∵
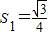
∴
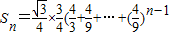
∴
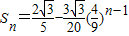
∴Mn的面积Sn的极限为
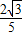
点评:本题以实际问题为载体,考查数列模型的构建,考查数列的极限,有一定的综合性.

练习册系列答案
相关题目

