网址:http://m.1010jiajiao.com/timu_id_4146[举报]
已知 ,(其中
,(其中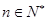 )
)
⑴求 及
及 ;
;
⑵试比较 与
与 的大小,并说明理由.
的大小,并说明理由.
【解析】第一问中取 ,则
,则 ;
…………1分
;
…………1分
对等式两边求导,得
取 ,则
,则 得到结论
得到结论
第二问中,要比较 与
与 的大小,即比较:
的大小,即比较: 与
与 的大小,归纳猜想可得结论当
的大小,归纳猜想可得结论当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, ;
;
猜想:当 时,
时, 运用数学归纳法证明即可。
运用数学归纳法证明即可。
解:⑴取 ,则
,则 ;
…………1分
;
…………1分
对等式两边求导,得 ,
,
取 ,则
,则 。 …………4分
。 …………4分
⑵要比较 与
与 的大小,即比较:
的大小,即比较: 与
与 的大小,
的大小,
当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, ;
…………6分
;
…………6分
猜想:当 时,
时, ,下面用数学归纳法证明:
,下面用数学归纳法证明:
由上述过程可知, 时结论成立,
时结论成立,
假设当 时结论成立,即
时结论成立,即 ,
,
当 时,
时,
而
∴
即 时结论也成立,
时结论也成立,
∴当 时,
时, 成立。
…………11分
成立。
…………11分
综上得,当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时,
查看习题详情和答案>>
(1)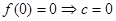 ,
,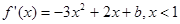 则
则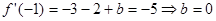 (4分)
(4分)
(2)由(1)知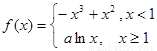 ,则
,则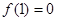
①当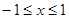 时,
时,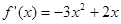 ,令
,令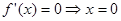 或
或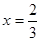
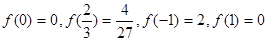 ,
,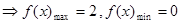
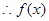 在
在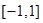 上的值域为
上的值域为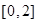 (7分)
(7分)
② 当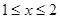 时,
a.若
时,
a.若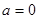 ,则
,则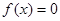
b.若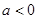 ,则
,则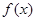 在
在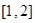 上是单调减的
上是单调减的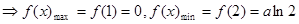
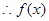 在
在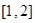 上的值域为
上的值域为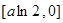
c.若 则
则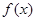 在
在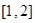 上是单调增的
上是单调增的
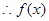 在
在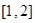 上的值域为
上的值域为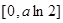 (9分)
(9分)
综上所述,当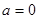 时,
时,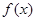 在
在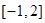 的值域为
的值域为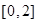
当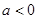 时,
时,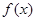 在
在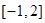 的值域为
的值域为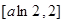 (10分)
(10分)
当 时,若
时,若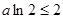
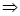
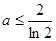 时,
时,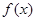 在
在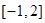 的值域为
的值域为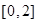
若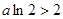
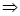
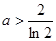 时,
时,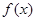 在
在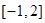 的值域为
的值域为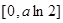 (12分)
(12分)
即 当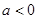 时,
时,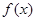 在
在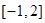 的值域为
的值域为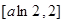
当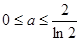 时,
时,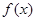 在
在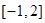 的值域为
的值域为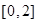
当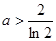 时,
时,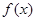 在
在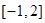 的值域为
的值域为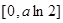
查看习题详情和答案>>
(1)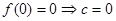 ,
,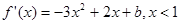 则
则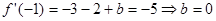 (4分)
(4分)
(2)由(1)知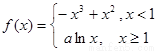 ,则
,则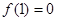
①当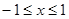 时,
时,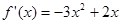 ,令
,令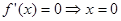 或
或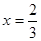
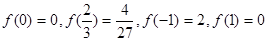 ,
,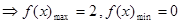
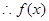 在
在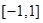 上的值域为
上的值域为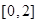 (7分)
(7分)
② 当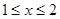 时,
a.若
时,
a.若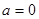 ,则
,则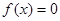
b.若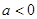 ,则
,则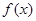 在
在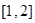 上是单调减的
上是单调减的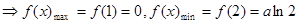
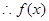 在
在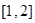 上的值域为
上的值域为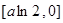
c.若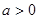 则
则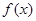 在
在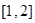 上是单调增的
上是单调增的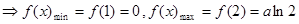
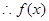 在
在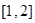 上的值域为
上的值域为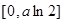 (9分)
(9分)
综上所述,当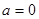 时,
时,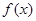 在
在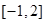 的值域为
的值域为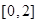
当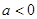 时,
时,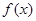 在
在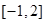 的值域为
的值域为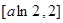 (10分)
(10分)
当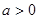 时,若
时,若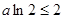
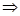
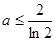 时,
时,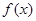 在
在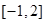 的值域为
的值域为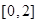
若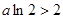
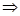
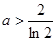 时,
时,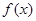 在
在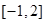 的值域为
的值域为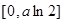 (12分)
(12分)
即 当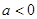 时,
时,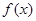 在
在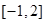 的值域为
的值域为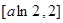
当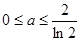 时,
时,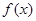 在
在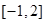 的值域为
的值域为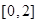
当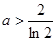 时,
时,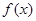 在
在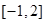 的值域为
的值域为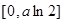
查看习题详情和答案>>
 和
和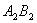 (看成两条互相平行的线段)分别长90米,甲在泳道
(看成两条互相平行的线段)分别长90米,甲在泳道 处出发,以
处出发,以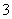 米/秒的速度到达
米/秒的速度到达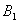 以同样的速度返回
以同样的速度返回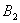 处出发,以
处出发,以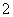 米/秒的速度到达
米/秒的速度到达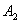 以同样的速度游回
以同样的速度游回 (Ⅰ)设甲离开池边
(Ⅰ)设甲离开池边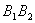 处的距离为
处的距离为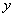 米,当时间
米,当时间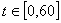 (单位:秒)时,写出
(单位:秒)时,写出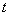 的函数解析式;
的函数解析式; (Ⅰ)设甲离开池边
(Ⅰ)设甲离开池边