网址:http://m.1010jiajiao.com/timu_id_409177[举报]
一、选择题:本大题共10小题,每小题5分,共50分,
1―5BADAD 6―10CBCAA
二、填空题:本大题共6小题,每小题5分,共24分。
数学理科.files/image257.gif)
17.
解:(1)数学理科.files/image259.gif)
数学理科.files/image261.gif)
数学理科.files/image263.gif)
所以数学理科.files/image265.gif)
(2)当数学理科.files/image183.gif) 时,
时,数学理科.files/image268.gif)
数学理科.files/image270.gif)
所以数学理科.files/image272.gif) ,即
,即数学理科.files/image274.gif) 。
。
(3)数学理科.files/image185.gif) 即
即数学理科.files/image277.gif) 所以
所以数学理科.files/image279.gif)
数学理科.files/image281.gif)
所以数学理科.files/image283.gif)
所以数学理科.files/image285.gif)
18. 解:(1)甲、乙两景点各有一个同学交换景点后,甲景点恰有2个A班同学有两种情况
① 互换的是A班同学,此时甲景点恰有2个A班的同学的事件记为数学理科.files/image287.gif) .
.
数学理科.files/image289.gif)
② ②互换的是B班同学,此时甲景点恰有2个A班的同学的事件记为数学理科.files/image291.gif) ..
..
数学理科.files/image293.gif)
所以甲景点恰有2个A班的同学的概率数学理科.files/image295.gif) .
.
(2) 甲景点内A班的同学数为数学理科.files/image188.gif) ,
,
则数学理科.files/image298.gif) ,
,数学理科.files/image300.gif) ,
,数学理科.files/image302.gif)
所以数学理科.files/image304.gif) 。
。
19. 解:(1)数学理科.files/image306.gif)
数学理科.files/image308.gif) 时,
时,数学理科.files/image310.gif) 取得最小值
取得最小值数学理科.files/image312.gif) ,
,
即数学理科.files/image314.gif)
(2)令数学理科.files/image316.gif)
由数学理科.files/image318.gif) ,得
,得数学理科.files/image320.gif) 或
或数学理科.files/image322.gif) (舍去)
(舍去)
数学理科.files/image324.gif)
(0,1)
1
(1,2)
数学理科.files/image326.gif)
数学理科.files/image328.gif)
0
数学理科.files/image330.gif)
数学理科.files/image332.gif)
增
极大值数学理科.files/image334.gif)
减
数学理科.files/image336.gif) 在
在数学理科.files/image338.gif) 内有最大值
内有最大值数学理科.files/image334.gif) ,
,
数学理科.files/image341.gif) 对
对数学理科.files/image197.gif) 时恒成立等价于
时恒成立等价于数学理科.files/image344.gif) 恒成立。
恒成立。
即数学理科.files/image346.gif)
数学理科.files/image348.gif)
20. (1)证明:以A为原点,AB,AD,AP所在直线为坐标轴建立直角坐标系(如图)
数学理科.files/image350.jpg)
则数学理科.files/image352.gif)
数学理科.files/image354.gif)
又数学理科.files/image356.gif)
所以数学理科.files/image358.gif) 面
面数学理科.files/image360.gif)
数学理科.files/image362.gif) 面
面数学理科.files/image360.gif) ,
,数学理科.files/image364.gif)
(2)解:数学理科.files/image366.gif) 面
面数学理科.files/image203.gif) ,
,数学理科.files/image210.gif) 与底面成
与底面成数学理科.files/image212.gif) 角,
角, 数学理科.files/image371.gif)
过E作数学理科.files/image373.gif) ,垂足为F,则
,垂足为F,则数学理科.files/image375.gif) ,
,数学理科.files/image377.gif)
数学理科.files/image379.gif) ,于是
,于是数学理科.files/image381.gif)
又数学理科.files/image383.gif)
则数学理科.files/image385.gif)
数学理科.files/image387.gif) 与
与数学理科.files/image222.gif) 所成角的余弦值为
所成角的余弦值为数学理科.files/image390.gif) 。
。
(3)设数学理科.files/image392.gif) 平面
平面数学理科.files/image224.gif) ,则
,则数学理科.files/image395.gif)
即数学理科.files/image397.gif)
数学理科.files/image399.gif)
令数学理科.files/image401.gif) 则
则数学理科.files/image403.gif)
A点到平面PCD的距离设为数学理科.files/image405.gif) ,则
,则数学理科.files/image407.gif)
即A点到平面PCD的距离设为数学理科.files/image409.gif) 。
。
21.
解:(1)在等比数列数学理科.files/image228.gif) 中,前
中,前数学理科.files/image230.gif) 项和为
项和为数学理科.files/image232.gif) ,若
,若数学理科.files/image236.gif) 成等差数列,则
成等差数列,则数学理科.files/image234.gif) 成等差数列。
成等差数列。
(2)数列数学理科.files/image228.gif) 的首项为
的首项为数学理科.files/image411.gif) ,公比为
,公比为数学理科.files/image413.gif) 。由题意知:
。由题意知:数学理科.files/image415.gif)
即数学理科.files/image417.gif)
数学理科.files/image419.gif)
当数学理科.files/image421.gif) 时,有
时,有数学理科.files/image423.gif)
显然:数学理科.files/image425.gif) 。此时逆命题为假。
。此时逆命题为假。
当数学理科.files/image427.gif) 时,有
时,有数学理科.files/image429.gif) ,
,
数学理科.files/image431.gif)
数学理科.files/image433.gif) ,此时逆命题为真。
,此时逆命题为真。
22.
解:(1)设椭圆方程为数学理科.files/image435.gif)
则数学理科.files/image437.gif) 解得
解得数学理科.files/image439.gif) 所以椭圆方程
所以椭圆方程数学理科.files/image441.gif)
(2)因为直线数学理科.files/image243.gif) 平行于OM,且在
平行于OM,且在数学理科.files/image116.gif) 轴上的截距为
轴上的截距为数学理科.files/image199.gif)
又数学理科.files/image446.gif) ,所以
,所以数学理科.files/image243.gif) 的方程为:
的方程为:数学理科.files/image448.gif)
由数学理科.files/image450.gif)
因为直线数学理科.files/image243.gif) 与椭圆交于
与椭圆交于数学理科.files/image249.gif) 两个不同点,
两个不同点,
数学理科.files/image453.gif)
所以数学理科.files/image199.gif) 的取值范围是
的取值范围是数学理科.files/image456.gif) 。
。
(3)设直线数学理科.files/image252.gif) 的斜率分别为
的斜率分别为数学理科.files/image459.gif) ,只要证明
,只要证明数学理科.files/image461.gif) 即可
即可
设数学理科.files/image463.gif) ,则
,则数学理科.files/image465.gif)
由数学理科.files/image467.gif)
可得数学理科.files/image469.gif)
而数学理科.files/image471.gif)
数学理科.files/image473.gif)
数学理科.files/image475.gif)
数学理科.files/image477.gif)
数学理科.files/image479.gif)
故直线MA、MB与数学理科.files/image054.gif) 轴始终围成一个等腰三角形。
轴始终围成一个等腰三角形。
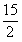 ,D、E两点分别在AB、AC上,使
,D、E两点分别在AB、AC上,使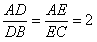 ,DE=3,现将△ABC沿DE折成直二角角,
,DE=3,现将△ABC沿DE折成直二角角,求:(Ⅰ)异面直线AD与BC的距离;
(Ⅱ)二面角A-EC-B的大小(用反三角函数表示)。

 中,
中, 两点分别在
两点分别在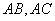 上。使
上。使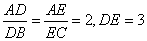 。将
。将 折成直二面角,则二面角
折成直二面角,则二面角 的余弦值为
的余弦值为 B.
B.  C.
C.  D.
D.

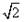 ,DE=4,现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合与点G,得到多面体CDEFG。
,DE=4,现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合与点G,得到多面体CDEFG。