摘要:(2)若的面积取得最大值时的椭圆方程.
网址:http://m.1010jiajiao.com/timu_id_407736[举报]
椭圆E的中心在原点O,焦点在x轴上,离心率e=
,过点C(-1,0)的直线l交椭圆于A、B两点,且满足:
=λ
(λ≥2).
(1)若λ为常数,试用直线l的斜率k(k≠0)表示三角形OAB的面积;
(2)若λ为常数,当三角形OAB的面积取得最大值时,求椭圆E的方程;
(3)若λ变化,且λ=k2+1,试问:实数λ和直线l的斜率k(k∈R)分别为何值时,椭圆E的短半轴长取得最大值?并求出此时的椭圆方程. 查看习题详情和答案>>
|
| CA |
| BC |
(1)若λ为常数,试用直线l的斜率k(k≠0)表示三角形OAB的面积;
(2)若λ为常数,当三角形OAB的面积取得最大值时,求椭圆E的方程;
(3)若λ变化,且λ=k2+1,试问:实数λ和直线l的斜率k(k∈R)分别为何值时,椭圆E的短半轴长取得最大值?并求出此时的椭圆方程. 查看习题详情和答案>>
椭圆![]() 的中心在原点
的中心在原点![]() ,焦点在
,焦点在![]() 轴上,
轴上,![]() ,过点
,过点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,且满足
两点,且满足![]() .
.
(1)若![]() 为常数,试用直线
为常数,试用直线![]() 的斜率
的斜率![]() 表示
表示![]() 的面积;
的面积;
(2)若![]() 为常数,当
为常数,当![]() 的面积取最大值时,求椭圆
的面积取最大值时,求椭圆![]() 的方程;
的方程;
(3)若![]() 变化且
变化且![]() ,试问:实数
,试问:实数![]() 和直线的斜率
和直线的斜率![]() 分别为何值时,椭圆
分别为何值时,椭圆![]() 的短半轴取得最大值,并求此时椭圆的方程.
的短半轴取得最大值,并求此时椭圆的方程.
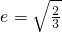 ,过点C(-1,0)的直线l交椭圆于A、B两点,且满足:
,过点C(-1,0)的直线l交椭圆于A、B两点,且满足: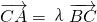 (λ≥2).
(λ≥2). ,过点C(-1,0)的直线l交椭圆于A、B两点,且满足:
,过点C(-1,0)的直线l交椭圆于A、B两点,且满足: (λ≥2).
(λ≥2).