网址：http://m.1010jiajiao.com/timu_id_403030[举报]
．如图所示，能承受最大拉力为10 N的细线OA与竖直方向成45°角，能承受最大拉力为5 N的细线OB水平，细线OC能承受足够大的拉力．为使OA、OB均不被拉断，OC下端所悬挂物体的最大重力是多少？
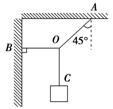
图4－2－27
【解析】：取O点为研究对象，受力分析如图所示．
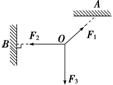
假设OB不会被拉断，且OA上的拉力先达到最大值，即F1＝10 N，根据平衡条件有F2＝F1max·cos45°＝10× N≈7.07 N，由于F2大于OB能承受的最大拉力，所以在物重逐渐增大时，细线OB先被拉断．再假设OB线上的拉力刚好达到最大值(即F2max＝5 N)，处于将被拉断的临界状态．根据平衡条件有F1cos45°＝F2max，F1sin45°＝F3，再选重物为研究对象，根据平衡条件有F3＝Gmax，以上三式联立解得悬挂物体的最大重力为Gmax＝F2max＝5 N.
查看习题详情和答案>>
(12分)如图所示，质量为5 kg的物块在水平拉力F＝15 N的作用下，从静止开始向右运动．物体与水平地面间的动摩擦因数μ＝0.2.求：
图3－17
(1)在力F的作用下，物体在前10 s内的位移；[来源:学+科+网]
(2)在t＝10 s末立即撤去力F，再经6 s物体还能运动多远？(g取10 m/s2)
【解析】：(1)物体在前10 s内受四个力：重力mg、支持力N、拉力F及滑动摩擦力f，如图所示．
根据牛顿第二定律有
N－mg＝0①
F－f＝ma1②
又f＝μN③
联立解得
a1＝＝ m/s2＝1 m/s2
由位移公式求出前10 s内的位移为
x1＝a1t2＝×1×102 m＝50 m.
(2)物体在10 s末的速度
v1＝a1t＝1×10 m/s＝10 m/s
10 s后物体做匀减速直线运动，其加速度大小为a2＝＝μg＝0.2×10 m/s2＝2 m/s2
要考虑物体做匀减速运动最长能运动多长时间，设最长还能运动的时间为t′
t′＝＝ s＝5 s.
可见，物体经5 s就停下，故6 s内的位移[来源:Zxxk.Com]
x2＝＝25 m.
查看习题详情和答案>>
．如图所示，能承受最大拉力为10 N的细线OA与竖直方向成45°角，能承受最大拉力为5 N的细线OB水平，细线OC能承受足够大的拉力．为使OA、OB均不被拉断，OC下端所悬挂物体的最大重力是多少？
图4－2－27
【解析】：取O点为研究对象，受力分析如图所示．
假设OB不会被拉断，且OA上的拉力先达到最大值，即F1＝10 N，根据平衡条件有F2＝F1max·cos45°＝10× N≈7.07 N，由于F2大于OB能承受的最大拉力，所以在物重逐渐增大时，细线OB先被拉断．再假设OB线上的拉力刚好达到最大值(即F2max＝5 N)，处于将被拉断的临界状态．根据平衡条件有F1cos45°＝F2max，F1sin45°＝F3，再选重物为研究对象，根据平衡条件有F3＝Gmax，以上三式联立解得悬挂物体的最大重力为Gmax＝F2max＝5 N.
查看习题详情和答案>>
(12分)如图所示，质量为5 kg的物块在水平拉力F＝15 N的作用下，从静止开始向右运动．物体与水平地面间的动摩擦因数μ＝0.2.求：
图3－17
(1)在力F的作用下，物体在前10 s内的位移；
(2)在t＝10 s末立即撤去力F，再经6 s物体还能运动多远？(g取10 m/s2)
【解析】：(1)物体在前10s内受四个力：重力mg、支持力N、拉力F及滑动摩擦力f，如图所示．
根据牛顿第二定律有
N－mg＝0①
F－f＝ma1②
又f＝μN③
联立解得
a1＝＝ m/s2＝1 m/s2
由位移公式求出前10 s内的位移为
x1＝a1t2＝×1×102 m＝50 m.
(2)物体在10 s末的速度
v1＝a1t＝1×10 m/s＝10 m/s
10 s后物体做匀减速直线运动，其加速度大小为a2＝＝μg＝0.2×10 m/s2＝2m/s2
要考虑物体做匀减速运动最长能运动多长时间，设最长还能运动的时间为t′
t′＝＝ s＝5 s.
可见，物体经5 s就停下，故6s内的位移
x2＝＝25 m.
查看习题详情和答案>>
（1）一物体静止在水平面上，它的质量是m，与水平面之间的动摩擦因数为μ．用平行于水平面的力F分别拉物体，得到加速度a和拉力F的关系图象如图所示．利用图象可求出这个物体的质量m．甲同学分析的过程是：从图象中得到F=12N时，物体的加速度a=4m/s2，根据牛顿定律导出：m=
| F |
| a |
乙同学的分析过程是：从图象中得出直线的斜率为：k=tan45°=1，而K=
| 1 |
| m |
请判断甲、乙两个同学结论的对和错，并分析错误的原因．如果两个同学都错，分析各自的错误原因后再计算正确的结果．
（2）两颗靠得很近的天体，离其他天体非常遥远，靠相互吸引力一起以连线上某一点为圆心分别作圆周运动，从而保持两者之间的距离不变，这样的天体称为“双星’．现测得两星中心间距离为R，运动周期为T，求：双星的总质量．
解：设双星的质量分别为M1、M2．它们绕其连线上的O点以周期T作匀速圆周运动，由万有引力定律及牛顿第二定律得：G
| M1M2 |
| R2 |
| 2π |
| T |
| M1M2 |
| R2 |
| 2π |
| T |
请判断上述解法是否正确，若正确，请完成计算；若不正确，请说明理由，并用你自己的方法算出正确结果．