摘要:(2)电梯匀速运动的速度 从图中读得.电梯匀速上升的时间t2=26s.电梯运动的总时间t=28s
网址:http://m.1010jiajiao.com/timu_id_402369[举报]
如图所示,长L1宽L2的矩形线圈,处于匀强磁场边缘,线圈与磁感线垂直,先后两次用力以v和2v的速度从图中位置把线圈匀速拉出磁场,则这两次( )
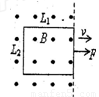
A、拉力之比为l:2
B、拉力的功率之比为l:2
C、线圈产生的电热之比为1:4
D、通过线圈某横截面的电量之比为l:l
查看习题详情和答案>>
如图所示,长L1宽L2的矩形线圈,处于匀强磁场边缘,线圈与磁感线垂直,先后两次用力以v和2v的速度从图中位置把线圈匀速拉出磁场,则这两次
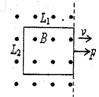
- A.拉力之比为l:2
- B.拉力的功率之比为l:2
- C.线圈产生的电热之比为1:4
- D.通过线圈某横截面的电量之比为1:1
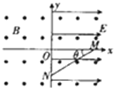 如图所示,坐标系xOy位于竖直平面内,空间中有沿水平方向、垂直纸而向外的匀强磁场,磁感应强度大小为B,在x>0的空间内有沿x轴正方向的匀强电场,电场强度大小为E.一带正电荷的小球从图中x轴上的M点沿着与水平方向成θ=30°角的斜向下的直线做匀速运动,进过y轴上的N点进入x<0的区域.要使小球进入x<0的区域后能在竖直面内做匀速圆周运动,需要在x<0的区域内另加一匀强电场.已知带电小球做圆周运动时通过y轴上的P点(P点未标出),重力加速度为g,求:
如图所示,坐标系xOy位于竖直平面内,空间中有沿水平方向、垂直纸而向外的匀强磁场,磁感应强度大小为B,在x>0的空间内有沿x轴正方向的匀强电场,电场强度大小为E.一带正电荷的小球从图中x轴上的M点沿着与水平方向成θ=30°角的斜向下的直线做匀速运动,进过y轴上的N点进入x<0的区域.要使小球进入x<0的区域后能在竖直面内做匀速圆周运动,需要在x<0的区域内另加一匀强电场.已知带电小球做圆周运动时通过y轴上的P点(P点未标出),重力加速度为g,求:(1)小球运动的速度大小;
(2)在x<0的区域内所加匀强电场的电场强度的大小和方向;
(3)N点与P点间的距离.
人移动时对绳的拉力不是恒力,重物不是做匀速运动也不是做匀变速运动,故无法用W=Fscosθ求对重物做的功,需从动能定理的角度来分析求解.
当绳下端由A点移到B点时,重物上升的高度为:h=
-H=
重力做功的数值为:WG=
当绳在B点实际水平速度为v时,v可以分解为沿绳斜向下的分速度v1和绕定滑轮逆时针转动的分速度v2,其中沿绳斜向下的分速度v1和重物上升速度的大小是一致的,
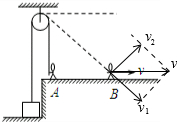
从图中可看出:v1=vcosθ
以重物为研究对象,根据动能定理得:W人-WG=
m
-0
解得:W人=
+
答:在这个过程中,人对重物做的功为
+
.
查看习题详情和答案>>
当绳下端由A点移到B点时,重物上升的高度为:h=
| H |
| sinθ |
| H(1-sinθ) |
| sinθ |
重力做功的数值为:WG=
| mgH(1-sinθ) |
| sinθ |
当绳在B点实际水平速度为v时,v可以分解为沿绳斜向下的分速度v1和绕定滑轮逆时针转动的分速度v2,其中沿绳斜向下的分速度v1和重物上升速度的大小是一致的,

从图中可看出:v1=vcosθ
以重物为研究对象,根据动能定理得:W人-WG=
| 1 |
| 2 |
| v | 21 |
解得:W人=
| mgH(1-sinθ) |
| sinθ |
| mv2cos2θ |
| 2 |
答:在这个过程中,人对重物做的功为
| mgH(1-sinθ) |
| sinθ |
| mv2cos2θ |
| 2 |
 (2011?湖南模拟)像打点计时器一样,光电计时器也是一种研究物体运动情况的常用计时仪器,其结构如图1所示,a、b分别是光电门的激光发射和接收装置,当有物体从a、b间通过时,光电计时器就可以显示物体的挡光时间.现利用图2所示装置测量滑块经过斜面上相隔lm左右的两个光电门时的速度,图中MN是水平桌面,Q是木板与桌面的接触点,1和2是固定在木板上适当位置的两个光电门,与之连接的两个光电计时器没有画出.让滑块从木板的顶端滑下,光电门l、2各自连接的计时器显示的挡光时间分别为5.0×10-2s和2.0×10-2s.用游标卡尺测量小滑块的宽度d,示数如图3所示.
(2011?湖南模拟)像打点计时器一样,光电计时器也是一种研究物体运动情况的常用计时仪器,其结构如图1所示,a、b分别是光电门的激光发射和接收装置,当有物体从a、b间通过时,光电计时器就可以显示物体的挡光时间.现利用图2所示装置测量滑块经过斜面上相隔lm左右的两个光电门时的速度,图中MN是水平桌面,Q是木板与桌面的接触点,1和2是固定在木板上适当位置的两个光电门,与之连接的两个光电计时器没有画出.让滑块从木板的顶端滑下,光电门l、2各自连接的计时器显示的挡光时间分别为5.0×10-2s和2.0×10-2s.用游标卡尺测量小滑块的宽度d,示数如图3所示.(1)读出滑块的宽度d=
5.015
5.015
cm;(2)滑块通过光电门1的速度v1=
1.0
1.0
m/s(计算结果保留两位有效数字),滑块通过光电门2的速度v2=2.5
2.5
m/s(计算结果保留两位有效数字).