网址:http://m.1010jiajiao.com/timu_id_392684[举报]
 同时满足:(1)各项均不为
同时满足:(1)各项均不为 ,(2)存在常数k, 对任意
,(2)存在常数k, 对任意 都成立,则称这样的数列
都成立,则称这样的数列 为“类等比数列” .由此等比数列必定是“类等比数列” .问:
为“类等比数列” .由此等比数列必定是“类等比数列” .问:(1)各项均不为0的等差数列
 是否为“类等比数列”?说明理由.
是否为“类等比数列”?说明理由.(2)若数列
 为“类等比数列”,且
为“类等比数列”,且 (a,b为常数),是否存在常数λ,使得
(a,b为常数),是否存在常数λ,使得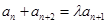 对任意
对任意 都成立?若存在,求出λ;若不存在,请举出反例.
都成立?若存在,求出λ;若不存在,请举出反例.(3)若数列
 为“类等比数列”,且
为“类等比数列”,且 ,
, (a,b为常数),求数列
(a,b为常数),求数列 的前n项之和
的前n项之和 ;数列
;数列 的前n项之和记为
的前n项之和记为 ,求
,求 .
.(1)当m=1时,求a2,a3,a4的值;
(2)是否存在实数m,使a2,a3,a4成等比数列?若存在,请求出实数m的值,并求出等比数列的公比;若不存在,请说明理由.
(3)设m=-1,f-1(x)为f(x)在x∈[0,+∞)的反函数,数列{bn}满足:b1=1,bn+1=f-1(bn2)(n∈N*),记Sn=b12+b22+…+bn2,求使Sn>2010成立的最小正整数n的值. 查看习题详情和答案>>
(1)当m=1时,求a2,a3,a4的值;
(2)是否存在实数m,使a2,a3,a4成等比数列?若存在,请求出实数m的值,并求出等比数列的公比;若不存在,请说明理由.
(3)设m=-1,f-1(x)为f(x)在x∈[0,+∞)的反函数,数列{bn}满足:b1=1,bn+1=f-1(bn2)(n∈N*),记Sn=b12+b22+…+bn2,求使Sn>2010成立的最小正整数n的值.
查看习题详情和答案>>
如图,电灯挂在圆桌的中央正上方,光学定理指出:桌边A处的照度I与射到点A的光线与桌面的夹角的正弦成正比,与点A到光源P的距离的平方成反比.已知桌面半径r=0.5 m,当光源与桌面相距1 m时,桌边A处的照度为I0,试写出照度I关于θ的函数表达式.

|