网址:http://m.1010jiajiao.com/timu_id_390898[举报]
[番茄花园1] 为了能更好地了解鲸的生活习性,某动物研究所在受伤的鲸身上安装了电子监测装置,从海岸放归点A处(如图所示)把它放归大海,并沿海岸线由西到东不停地对鲸进行了40分钟的跟踪观测,每隔10分钟踩点测得数据如下表(设鲸沿海面游动)。然后又在观测站B处对鲸进行生活习性的详细观测。已知AB=15km,观测站B的观测半径为5km.

观测时刻t (分钟) |
跟踪观测点到放归点距离a(km) |
鲸位于跟踪观测点正北方向的距离b(km) |
|
10 |
1 |
1 |
|
20 |
2 |
|
|
30 |
3 |
|
|
40 |
4 |
2 |
(I)根据表中数据:(1)计算鲸沿海岸线方向运动的速度,(2)写出a、b满足的关系式,并画出鲸的运动路线简图;
(II)若鲸继续以(I)-(2)中的运行路线运动,则鲸经过多少分钟(从放归时计时),可进入前方观测站B的观测范围。()
[番茄花园1]18.
查看习题详情和答案>>零件直径相等的概率。本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识,考查数据处理能力及运用概率知识解决简单的实际问题的能力。满分12分
【解析】(Ⅰ)解:由所给数据可知,一等品零件共有6个.设“从10个零件中,随机抽取一个为一等品”为事件A,则P(A)=![]() =
=![]() .
.
(Ⅱ)(i)解:一等品零件的编号为![]() .从这6个一等品零件中随机抽取2个,所有可能的结果有:
.从这6个一等品零件中随机抽取2个,所有可能的结果有:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 共有15种.
共有15种.
(ii)解:“从一等品零件中,随机抽取的2个零件直径相等”(记为事件B)的所有可能结果有:![]() ,
,![]() ,共有6种.
,共有6种.
所以P(B)=![]() .
.
(本小题满分12分)
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=![]() ,∠BAD=∠CDA=45°.
,∠BAD=∠CDA=45°.
 (Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅱ)证明CD⊥平面ABF;
(Ⅲ)求二面角B-EF-A的正切值。
查看习题详情和答案>>零件直径相等的概率。本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识,考查数据处理能力及运用概率知识解决简单的实际问题的能力。满分12分
【解析】(Ⅰ)解:由所给数据可知,一等品零件共有6个.设“从10个零件中,随机抽取一个为一等品”为事件A,则P(A)=![]() =
=![]() .
.
(Ⅱ)(i)解:一等品零件的编号为![]() .从这6个一等品零件中随机抽取2个,所有可能的结果有:
.从这6个一等品零件中随机抽取2个,所有可能的结果有:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 共有15种.
共有15种.
(ii)解:“从一等品零件中,随机抽取的2个零件直径相等”(记为事件B)的所有可能结果有:![]() ,
,![]() ,共有6种.
,共有6种.
所以P(B)=![]() .
.
(本小题满分12分)
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=![]() ,∠BAD=∠CDA=45°.
,∠BAD=∠CDA=45°.
 (Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅱ)证明CD⊥平面ABF;
(Ⅲ)求二面角B-EF-A的正切值。
查看习题详情和答案>>为了解高中一年级学生身高情况,某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查,测得身高频数分布表如下表1、表2.
表1:男生身高频数分布表
|
身高(cm) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
[180,185) |
[185,190) |
|
频数 |
2 |
5 |
14 |
13 |
4 |
2 |
表2:女生身高频数分布表
|
身高(cm) |
[150,155) |
[155,160) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
|
频数 |
1 |
7 |
12 |
6 |
3 |
1 |
(I)求该校男生的人数并完成下面频率分布直方图;

(II)估计该校学生身高在 的概率;
的概率;
(III)从样本中身高在180 190cm之间的男生中任选2人,求至少有1人身高在185
190cm之间的男生中任选2人,求至少有1人身高在185 190cm之间的概率。
190cm之间的概率。
【解析】第一问样本中男生人数为40 ,
由分层抽样比例为10%可得全校男生人数为400
(2)中由表1、表2知,样本中身高在 的学生人数为:5+14+13+6+3+1=42,样本容量为70 ,所以样本中学生身高在
的学生人数为:5+14+13+6+3+1=42,样本容量为70 ,所以样本中学生身高在 的频率
的频率
故由 估计该校学生身高在
估计该校学生身高在 的概率
的概率
(3)中样本中身高在180 185cm之间的男生有4人,设其编号为①②③④ 样本中身高在185
185cm之间的男生有4人,设其编号为①②③④ 样本中身高在185 190cm之间的男生有2人,设其编号为⑤⑥从上述6人中任取2人的树状图,故从样本中身高在180
190cm之间的男生有2人,设其编号为⑤⑥从上述6人中任取2人的树状图,故从样本中身高在180 190cm之间的男生中任选2人得所有可能结果数为15,求至少有1人身高在185
190cm之间的男生中任选2人得所有可能结果数为15,求至少有1人身高在185 190cm之间的可能结果数为9,因此,所求概率
190cm之间的可能结果数为9,因此,所求概率
由表1、表2知,样本中身高在 的学生人数为:5+14+13+6+3+1=42,样本容量为70 ,所以样本中学生身高在
的学生人数为:5+14+13+6+3+1=42,样本容量为70 ,所以样本中学生身高在
的频率
 -----------------------------------------6分
-----------------------------------------6分
故由 估计该校学生身高在
估计该校学生身高在 的概率
的概率 .--------------------8分
.--------------------8分
(3)样本中身高在180 185cm之间的男生有4人,设其编号为①②③④ 样本中身高在185
185cm之间的男生有4人,设其编号为①②③④ 样本中身高在185 190cm之间的男生有2人,设其编号为⑤⑥从上述6人中任取2人的树状图为:
190cm之间的男生有2人,设其编号为⑤⑥从上述6人中任取2人的树状图为:

--10分
故从样本中身高在180 190cm之间的男生中任选2人得所有可能结果数为15,求至少有1人身高在185
190cm之间的男生中任选2人得所有可能结果数为15,求至少有1人身高在185 190cm之间的可能结果数为9,因此,所求概率
190cm之间的可能结果数为9,因此,所求概率
查看习题详情和答案>>
某地区对12岁儿童瞬时记忆能力进行调查.瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果.例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人.
|
|
视觉记忆能力 |
||||
|
偏低 |
中等 |
偏高 |
超常 |
||
|
听觉 记忆 能力 |
偏低 |
0 |
7 |
5 |
1 |
|
中等 |
1 |
8 |
3 |
|
|
|
偏高 |
2 |
|
0 |
1 |
|
|
超常 |
0 |
2 |
1 |
1 |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为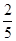 .
.
(I)试确定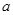 、
、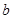 的值;
的值;
(II)从40人中任意抽取3人,求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率;
(III)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为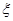 ,求随机变量
,求随机变量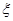 的数学期望
的数学期望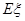 .
.
【解析】1)中由表格数据可知,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的学生共有(10+a)人.记“视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上”为事件A,则P(A)=(10+a)/40=2/5,解得a=6.……………2分
所以.b=40-(32+a)=40-38=2答:a的值为6,b的值为2.………………3分
(2)中由表格数据可知,具有听觉记忆能力或视觉记忆能力超常的学生共有8人.
方法1:记“至少有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件B,
则“没有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件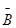
(3)中由于从40位学生中任意抽取3位的结果数为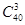 ,其中具有听觉记忆能力或视觉记忆能力偏高或超常的学生共24人,从40位学生中任意抽取3位,其中恰有k位具有听觉记忆能力或视觉记忆能力偏高或超常的结果数为
,其中具有听觉记忆能力或视觉记忆能力偏高或超常的学生共24人,从40位学生中任意抽取3位,其中恰有k位具有听觉记忆能力或视觉记忆能力偏高或超常的结果数为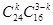 ,………………………7分
,………………………7分
所以从40位学生中任意抽取3位,其中恰有k位具有听觉记忆能力或视觉记忆能力偏高或超常的概率为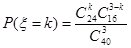 ,k=0,1,2,3
,k=0,1,2,3
查看习题详情和答案>>
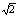
 视觉
[来源:]
视觉
[来源:]