摘要:由已知和= f(). 5分
网址:http://m.1010jiajiao.com/timu_id_39052[举报]
(本小题满分14分)
已知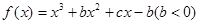 在[-1,0]和[0,2]上有相反的单调性.
在[-1,0]和[0,2]上有相反的单调性.
(Ⅰ)求c的值;
(Ⅱ)若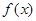 的图象上在两点
的图象上在两点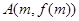 、
、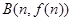 处的切线都与y轴垂直,且函数f(x)在区间[m,n]上存在零点,求实数b的取值范围;
处的切线都与y轴垂直,且函数f(x)在区间[m,n]上存在零点,求实数b的取值范围;
(Ⅲ)若函数f(x)在[0,2]和[4,5]上有相反的单调性,在f(x)的图象上是否存在一点M,使得f(x)在点M的切线斜率为2b?若存在,求出M点坐标;若不存在,请说明理由.
查看习题详情和答案>>
(本小题满分14分)
已知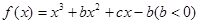 在[-1,0]和[0,2]上有相反的单调性.
在[-1,0]和[0,2]上有相反的单调性.
(Ⅰ)求c的值;
(Ⅱ)若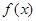 的图象上在两点
的图象上在两点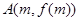 、
、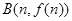 处的切线都与y轴垂直,且函数f(x)在区间[m,n]上存在零点,求实数b的取值范围;
处的切线都与y轴垂直,且函数f(x)在区间[m,n]上存在零点,求实数b的取值范围;
(Ⅲ)若函数f(x)在[0,2]和[4,5]上有相反的单调性,在f(x)的图象上是否存在一点M,使得f(x)在点M的切线斜率为2b?若存在,求出M点坐标;若不存在,请说明理由.
查看习题详情和答案>>
(2006•朝阳区二模)设对于任意实数x、y,函数f(x)、g(x)满足f(x+1)=
f(x),且f(0)=3,g(x+y)=g(x)+2y,g(5)=13,n∈N*.
(Ⅰ)求数列{f(n)}、{g(n)}的通项公式;
(Ⅱ)设cn=g[
f(n)],求数列{cn}的前n项和Sn;
(Ⅲ)已知
=0,设F(n)=Sn-3n,是否存在整数m和M,使得对任意正整数n不等式m<F(n)<M恒成立?若存在,分别求出m和M的集合,并求出M-m的最小值;若不存在,请说明理由.
查看习题详情和答案>>
| 1 |
| 3 |
(Ⅰ)求数列{f(n)}、{g(n)}的通项公式;
(Ⅱ)设cn=g[
| n |
| 2 |
(Ⅲ)已知
| lim | ||
| n |
| 2n+3 |
| 3n-1 |
 ax2+3x.
ax2+3x. ax2+3x.
ax2+3x.