网址:http://m.1010jiajiao.com/timu_id_390208[举报]
已知函数 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)设 ,若对任意
,若对任意 ,
, ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【解析】第一问利用 的定义域是
的定义域是

由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函数 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是
第二问中,若对任意 不等式
不等式 恒成立,问题等价于
恒成立,问题等价于 只需研究最值即可。
只需研究最值即可。
解: (I) 的定义域是
的定义域是 ......1分
......1分
 ............. 2分
............. 2分
由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函数 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是 ........4分
........4分
(II)若对任意 不等式
不等式 恒成立,
恒成立,
问题等价于 ,
.........5分
,
.........5分
由(I)可知,在 上,x=1是函数极小值点,这个极小值是唯一的极值点,
上,x=1是函数极小值点,这个极小值是唯一的极值点,
故也是最小值点,所以 ; ............6分
; ............6分

当b<1时, ;
;
当 时,
时, ;
;
当b>2时, ;
............8分
;
............8分
问题等价于
 ........11分
........11分
解得b<1 或 或
或  即
即 ,所以实数b的取值范围是
,所以实数b的取值范围是
查看习题详情和答案>>
已知函数 在
在 处取得极值2.
处取得极值2.
⑴ 求函数 的解析式;
的解析式;
⑵ 若函数 在区间
在区间 上是单调函数,求实数m的取值范围;
上是单调函数,求实数m的取值范围;
【解析】第一问中利用导数
又f(x)在x=1处取得极值2,所以 ,
,
所以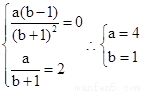
第二问中,
因为 ,又f(x)的定义域是R,所以由
,又f(x)的定义域是R,所以由 ,得-1<x<1,所以f(x)在[-1,1]上单调递增,在
,得-1<x<1,所以f(x)在[-1,1]上单调递增,在 上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有
上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有 ,得
,得
解:⑴ 求导 ,又f(x)在x=1处取得极值2,所以
,又f(x)在x=1处取得极值2,所以 ,即
,即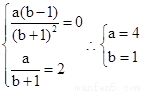 ,所以
,所以 …………6分
…………6分
⑵ 因为 ,又f(x)的定义域是R,所以由
,又f(x)的定义域是R,所以由 ,得-1<x<1,所以f(x)在[-1,1]上单调递增,在
,得-1<x<1,所以f(x)在[-1,1]上单调递增,在 上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有
上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有 ,得
,得 , …………9分
, …………9分
当f(x)在区间(m,2m+1)上单调递减,则有
得 …………12分
…………12分
.综上所述,当 时,f(x)在(m,2m+1)上单调递增,当
时,f(x)在(m,2m+1)上单调递增,当 时,f(x)在(m,2m+1)上单调递减;则实数m的取值范围是
时,f(x)在(m,2m+1)上单调递减;则实数m的取值范围是 或
或
查看习题详情和答案>>
已知下表为函数f(x)=ax3+cx+d部分自变量取值及其对应函数值,为便于研究,相关函数值非整数值时,取值精确到0.01.
(1)f(x)为奇函数; (2)f(x)在[0.55,0.6]上必有零点 (3)f(x)在(-∞,-0.35]上单调递减; (4)a<0 其中所有正确命题的个数是( ) |
| x | 3.27 | 1.57 | -0.61 | -0.59 | 0.26 | 0.42 | -0.35 | -0.56 | 4.25 | |
| y | -101.63 | -10.04 | 0.07 | 0.026 | 0.21 | 0.20 | -0.22 | -0.03 | -226.05 |
(1)f(x)为奇函数; (2)f(x)在[0.55,0.6]上必有零点
(3)f(x)在(-∞,-0.35]上单调递减; (4)a<0
其中所有正确命题的个数是( )
A.4
B.3
C.2
D.1
查看习题详情和答案>>
已知下表为函数f(x)=ax3+cx+d部分自变量取值及其对应函数值,为便于研究,相关函数值非整数值时,取值精确到0.01.
| x | 3.27 | 1.57 | -0.61 | -0.59 | 0.26 | 0.42 | -0.35 | -0.56 | 0 | 4.25 |
| y | -101.63 | -10.04 | 0.07 | 0.026 | 0.21 | 0.20 | -0.22 | -0.03 | 0 | -226.05 |
(1)f(x)为奇函数; (2)f(x)在[0.55,0.6]上必有零点
(3)f(x)在(-∞,-0.35]上单调递减; (4)a<0
其中所有正确命题的个数是
- A.4
- B.3
- C.2
- D.1