网址:http://m.1010jiajiao.com/timu_id_386460[举报]
2. D. 由直方图的意义即可直接求得结果.
4. A. 显然函数是偶函数,排除C.函数图象经过原点O,于是排除B.当.files/image208.gif) 时,函数
时,函数.files/image210.gif) ,其图象可由函数
,其图象可由函数.files/image212.gif) 的图象向左平移一个单位得到,故选A.
的图象向左平移一个单位得到,故选A.
5.
C. 六个小组每小组4个队, 进行单循环赛的比赛场次一共有 6.files/image214.gif) ,16个队进行淘汰赛比赛场次一共有
,16个队进行淘汰赛比赛场次一共有.files/image216.gif) 确定冠亚军一共需比赛
确定冠亚军一共需比赛.files/image218.gif) 场次, 故选C.
场次, 故选C.
.files/image220.gif)
6.B.如图所示,.files/image222.gif) 就是二面角
就是二面角.files/image224.gif) 的平面角,由图知
的平面角,由图知.files/image222.gif) 的取值范围是
的取值范围是.files/image227.gif) .
.
7. B. 依题意得,.files/image229.gif) 若
若.files/image231.gif) ,则
,则.files/image233.gif) 于是
于是
.files/image237.gif) 又
又
.files/image239.gif) ,解得
,解得.files/image241.gif) .
.
8. C. 因为2009于2007不能被4整除,先排除A.D.又2100不能被400整除,所以2100不是闰年,排除B.从而选C.
9. B.设首项为.files/image243.gif) 公差为
公差为.files/image245.gif) ,则
,则.files/image247.gif)
.files/image249.gif) 。于是
。于是.files/image251.gif) 过点
过点.files/image253.gif) 和
和.files/image255.gif) 的直线斜率为
的直线斜率为.files/image257.gif) 则过点
则过点.files/image253.gif) 和
和.files/image255.gif) 的直线的一个方向向量的坐标应选B.
的直线的一个方向向量的坐标应选B.
10.
D. 易知点B在第一或第四象限.设过点A的直线与曲线C相切于点.files/image259.gif) , 则切线斜率为
, 则切线斜率为.files/image261.gif) ,则
,则.files/image263.gif) , 则切点为
, 则切点为.files/image265.gif) ,
,.files/image267.gif) 要使视线不被C挡住,必须满足
要使视线不被C挡住,必须满足.files/image269.gif)
.files/image271.gif) 故选D.
故选D.
11.6.由.files/image090.gif)
.files/image273.gif) .
.
.files/image285.gif)
13.
.files/image287.gif) .点P的坐标有36种,而圆内部点的坐标必须满足
.点P的坐标有36种,而圆内部点的坐标必须满足.files/image289.gif) 则点P落在圆
则点P落在圆.files/image094.gif) 的内部的坐标种数为8种,
的内部的坐标种数为8种,
所以由等可能事件的概率计算公式得所求概率为.files/image291.gif) .
.
14.6.依题意得.files/image293.gif)
.files/image295.gif) 显然函数
显然函数.files/image108.gif) 的最大值为6.
的最大值为6.
15. 1, 3, 1. A处在9×9的九宫格子中的第2行,第3列,按照1到9的数字在每一行只能出现一次知,A处不能填入3,5,7,9;按照1到9的数字在每一列中只能出现一次知,A处不能填入2,4,6,8,综合知A处只能填入1.同理分析知C处只能填入1.B处只能填入3.
16(Ⅰ).files/image298.gif)
.files/image300.gif)
.files/image302.gif) 当
当.files/image304.gif) ,
,
(Ⅱ) 将.files/image311.gif) 的图像依次进行如下变换:
的图像依次进行如下变换:
1.把函数.files/image311.gif) 的图像向下平移
的图像向下平移.files/image188.gif) 个单位长度,得到函数
个单位长度,得到函数.files/image314.gif) 的图像;
的图像;
2.把得到的函数图像上各点横坐标缩短到原来的.files/image188.gif) 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数.files/image316.gif) 的图像;
的图像;
3.将函数.files/image316.gif) 的图像向右平移
的图像向右平移.files/image318.gif) 个单位长度,
个单位长度,
就得到函数.files/image320.gif) 的图像.
的图像.
或按如下平移变换:
1.把函数.files/image311.gif) 的图像向下平移
的图像向下平移.files/image188.gif) 个单位长度,得到函数
个单位长度,得到函数.files/image314.gif) 的图像;
的图像;
2.将函数.files/image314.gif) 的图像向右平移
的图像向右平移.files/image322.gif) 个单位长度,就得到函数
个单位长度,就得到函数
.files/image324.gif) 的图像.
的图像.
3.把得到的函数.files/image324.gif) 图像上各点横坐标缩短到原来的
图像上各点横坐标缩短到原来的.files/image188.gif) 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数.files/image320.gif) 的图像
的图像
17.(I)由等可能事件的概率意义及概率计算公式得P==; 3分
(II)设选取的5只福娃恰好距离组成完整“奥运会吉祥物”差一种福娃记为事件
A,差两种福娃记为事件B, 依题意可知,所选5只福娃恰好距离组成完整“奥运会
吉祥物”最多差2只,则
.files/image326.gif) 7分
7分
.files/image328.gif) 10分
10分
故选取的5只福娃距离组成完整“奥运会吉祥物”至少差一种福娃的概率为
18.解法一:(1)如图:
.files/image336.jpg)
.files/image338.gif)
.files/image340.gif)
.files/image342.gif) 故
故.files/image344.gif) .所以
.所以.files/image346.gif) .又
.又.files/image348.gif) .
.
故.files/image350.gif)
故当.files/image356.gif) 时,直线
时,直线.files/image358.gif) .
.
(Ⅱ)依题意,要在.files/image360.gif) 上找一点
上找一点.files/image132.gif) ,使得
,使得.files/image363.gif) .可推测
.可推测.files/image360.gif) 的中点
的中点.files/image365.gif) 即为所求的
即为所求的.files/image132.gif) 点.因为
点.因为.files/image367.gif)
.files/image369.gif) ,所以
,所以.files/image371.gif)
又.files/image373.gif) ,故
,故.files/image375.gif) .
.
从而.files/image377.gif)
解法二:(1)建立如图所示的空间直角坐标系,
.files/image379.jpg)
则A(1,0,0), B(1,1,0), P(0,1,m),C(0,1,0), D(0,0,0), B1(1,1,1), D1(0,0,1).
所以.files/image381.gif)
.files/image383.gif)
又由.files/image385.gif) 的一个法向量.
的一个法向量.
则.files/image392.gif)
依题意有:.files/image394.gif) ,解得
,解得.files/image356.gif) .
.
故当.files/image356.gif) 时,直线
时,直线.files/image358.gif) .
.
则.files/image400.gif) .依题意,对任意的m要使D1Q在平面APD1上的射影垂直于AP.等价于
.依题意,对任意的m要使D1Q在平面APD1上的射影垂直于AP.等价于
.files/image402.gif) ,即
,即.files/image132.gif) 为
为.files/image360.gif) 的中点时,满足题设的要求
的中点时,满足题设的要求
19.(Ⅰ) .files/image404.gif) ,由
,由.files/image143.gif) 得
得.files/image406.gif) ,
,
所以.files/image408.gif) .由
.由.files/image410.gif) 得
得.files/image412.gif) 或
或.files/image414.gif)
-2
.files/image417.gif)
-1
.files/image419.gif)
.files/image421.gif)
2
.files/image423.gif)
0
0
.files/image108.gif)
0
递增
递减
递增
0
由上表知:.files/image108.gif) 在区间
在区间.files/image146.gif) 上的最大值为
上的最大值为.files/image428.gif) ,最小值为
,最小值为.files/image430.gif) .
(Ⅱ)
.
(Ⅱ).files/image404.gif) 的图像为开口向上且过点
的图像为开口向上且过点.files/image433.gif) 的抛物线,由条件
的抛物线,由条件.files/image435.gif) ,
,.files/image437.gif) ,即
,即.files/image439.gif) 得
得.files/image441.gif)
20. (1)解:由.files/image443.gif) 知:
知:.files/image445.gif) ,
,
而.files/image447.gif) ,
,.files/image449.gif) ,解得
,解得.files/image451.gif) 2分
2分
令.files/image453.gif) ,得
,得.files/image455.gif) ,即
,即.files/image457.gif) R) 4分
R) 4分
(2)解:令.files/image459.gif) ,∴
,∴.files/image461.gif) ,即
,即.files/image463.gif) .
.
当.files/image465.gif) 时,
时,.files/image467.gif) ,
,
当n≥2时,.files/image469.gif) .
.
综合得:.files/image471.gif) 6分
6分
由题意:.files/image473.gif) ,变形得:
,变形得:.files/image475.gif) ,
,
∴数列.files/image477.gif) 是以
是以.files/image479.gif) 为公比,
为公比,.files/image481.gif) 为首项的等比数列.
为首项的等比数列.
.files/image483.gif) ,即
,即.files/image485.gif) . 9分
. 9分
(3)解:当.files/image487.gif) (
(.files/image489.gif) N*)时,
N*)时,
.files/image491.gif)
.files/image493.gif) 11分
11分
当.files/image495.gif) (
(.files/image489.gif) N*)时,
N*)时,
.files/image497.gif)
.files/image499.gif) . 13分
. 13分
21.(I)依题意,设P(t,2)(-2≤t≤2),M(x,y).
当t=0时,点M与点E重合,则M=(0,1);
当t≠0时,线段OP的垂直平分线方程为:.files/image501.gif)
.files/image503.gif)
显然,点(0,1)适合上式 .故点M的轨迹方程为x2=-4(y-1)( -2≤x≤2)
(II)设.files/image505.gif) 得x2+4k-2=0.
得x2+4k-2=0.
设Q(x1,y1)、R(x2,y2),则.files/image507.gif)
.files/image509.gif) ,
,.files/image511.gif) .消去x2,得
.消去x2,得.files/image513.gif) .
.
.files/image515.gif)
解得.files/image517.gif)
(本大题满分13分)
在△ABC中,![]() ,点B是椭圆
,点B是椭圆![]() 的上顶点,l是双曲线
的上顶点,l是双曲线![]() 位于x轴下方的准线,当AC在直线l上运动时.
位于x轴下方的准线,当AC在直线l上运动时.
(1)求△ABC外接圆的圆心![]() 的轨迹E的方程;
的轨迹E的方程;
(2)过定点F(0,![]() )作互相垂直的直线l1、l2,分别交轨迹E于点M、N和点R、Q.求四边形MRNQ的面积的最小值.
)作互相垂直的直线l1、l2,分别交轨迹E于点M、N和点R、Q.求四边形MRNQ的面积的最小值.
20.(本大题满分13分)
在△ABC中,![]() ,点B是椭圆
,点B是椭圆![]() 的上顶点,l是双曲线
的上顶点,l是双曲线![]() 位于x轴下方的准线,当AC在直线l上运动时.
位于x轴下方的准线,当AC在直线l上运动时.
(1)求△ABC外接圆的圆心![]() 的轨迹E的方程;
的轨迹E的方程;
(2)过定点F(0,![]() )作互相垂直的直线l1、l2,分别交轨迹E于点M、N和点R、Q.求四边形MRNQ的面积的最小值.
)作互相垂直的直线l1、l2,分别交轨迹E于点M、N和点R、Q.求四边形MRNQ的面积的最小值.
.files/image194.gif)
.files/image196.gif) ,且
,且.files/image198.gif) ,
,.files/image201.gif) .
. .files/image203.gif) 知,函数
知,函数.files/image206.gif) 选B.
选B..files/image235.gif) 而
而.files/image275.gif)
.files/image277.gif) .取
.取.files/image279.gif) 取
取.files/image281.gif)
.files/image283.gif)
.files/image306.gif)
.files/image308.gif)
.files/image330.gif)
.files/image332.gif)
.files/image334.gif)
.files/image352.gif)
.files/image354.gif) ,即
,即.files/image124.gif)
.files/image388.gif)
.files/image390.gif)
.files/image398.gif) ,
, ,设
,设 ,数列
,数列 .
.  是等差数列;
是等差数列; 的前n项和Sn;
的前n项和Sn; 一切正整数n恒成立,求实数m的取值范围.
一切正整数n恒成立,求实数m的取值范围. 的扇形铁皮
的扇形铁皮 ,欲从其中裁剪出一块内接五边形
,欲从其中裁剪出一块内接五边形 ,使点
,使点 在
在 弧上,点
弧上,点 分别在半径
分别在半径 和
和 上,四边形
上,四边形 是矩形,点
是矩形,点 在弧
在弧 上,
上, 点在线段
点在线段 上,四边形
上,四边形 是直角梯形.现有如下裁剪方案:先使矩形
是直角梯形.现有如下裁剪方案:先使矩形 ,当矩形
,当矩形 的值;
的值;
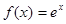 ,过该函数图象上点
,过该函数图象上点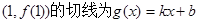
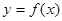 图象上的点总在
图象上的点总在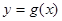 图象的上方;
图象的上方;
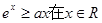 上恒成立,求实数
上恒成立,求实数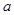 的取值范围.
的取值范围.