网址:http://m.1010jiajiao.com/timu_id_378815[举报]
一、选择题:
1―12题DABBA CBCBD DC
二、填空题:
13、31或40
14、乙
15、5
16、③④
三、解答题:
∵m•n=1
(II)∵(
18、解:(I)设“甲射击一次命中”为事件A,“乙射击一次命中”为事件B
ξ可能的取值为0,1,2,3,故
故ξ的分布列为
ξ
0
1
2
3
P
19、解:(I)设等比数列{an}的首项为a1,公比为q,
依题意,有2(a3+2)=a2+a4,
代入a2+a3+a4=28, 得a3=8,
∴a2+a4=20┉┉┉┉┉┉┉┉2分
又{an}单调递增,∴q=2,a1=2,
∴an=2n ┉┉┉┉┉┉┉┉6分
20、(I)证明:在直棱柱ABC-A1B
∵ ∠ACB=90º,∴A
∵CG.files/image187.gif) 平面C1CBB1,∴A
平面C1CBB1,∴A
在矩形C1CBB1中,CC1=BB1=2BC,G为BB1的中点,
∴∠CGC1=90,即CG⊥C
而A
∴CG⊥平面A1GC1。
∴平面A1CG⊥平面A1GC1。┉┉┉┉┉┉┉┉6分
(II)由于CC1平面ABC,
∠ACB=90º,建立如图所示的空间坐标系,设AC=BC=CC1=a,则A(a,0,0),B(0,a,0)
A1(a,0,
∴.files/image192.gif) =(a,0,
=(a,0,.files/image194.gif) =(0,a,a). ┉┉┉┉┉┉┉┉8分
=(0,a,a). ┉┉┉┉┉┉┉┉8分
设平面A1CG的法向量n1=(x1,y1,z1),
令z1=1,n1=(-2,-1,1). ┉┉┉┉┉┉┉┉9分
又平面ABC的法向量为n2=(0,0,1) ┉┉┉┉┉┉┉┉10分
设平面ABC与平面A1CG所成锐二面角的平面角为θ,
即平面ABC与平面A1CG所成锐二面角的平面角的余弦值为.files/image202.gif) 。┉┉┉12分
。┉┉┉12分
21、解:(I)∵△ABM是边长为2的正三角形,∴圆M的半径r=2,┉┉┉┉┉┉1分
又圆M与x轴相切,∴当x=c时,得y=.files/image205.gif) ,r=
,r=.files/image207.gif) ┉┉┉┉┉┉┉┉3分
┉┉┉┉┉┉┉┉3分
∵.files/image211.gif) 解得a=3或a=-1(舍去),则b2=
解得a=3或a=-1(舍去),则b2=
(2)设C(x1,y1),D(x2,y2)。
∵c=1, ∴a2=b2+c2>1,
②当直线CD不与x轴重合时,设直线CD的方程为x=my+1,代入.files/image098.gif)
∴x1x2+y1y2=(m2+1)y1y2+m(y1+y2)+1=.files/image229.gif)
.files/image231.gif) +1
+1
∴a>0,b>0, ∴a<b2,即a<a2-1, ∴a2-a-1>0.
由①②可知,a的取值范围是(.files/image255.gif) ,+∞) ┉┉┉┉┉┉┉┉12分
,+∞) ┉┉┉┉┉┉┉┉12分
22、(1)由a=0,f(x)≥h(x)可得-mlnx≥-x
(2)函数k(x)=f(x)-h(x)在[1,3]上恰有两个不同的零点等价于方程x-2lnx=a,在[1,3]上恰有两个相异实根。┉┉┉┉┉┉┉┉5分
又g(1)=1,g(3)=3-2ln3
∵g(1)>g(3),∴只需g(2)<a≤g(3),
故a的取值范围是(2-2ln2,3-2ln3) ┉┉┉┉┉┉┉┉9分
(3)存在m=.files/image096.gif) ,使得函数f(x)和函数h(x)在公共定义域上具有相同的单调性
,使得函数f(x)和函数h(x)在公共定义域上具有相同的单调性
若.files/image296.gif) ,则
,则.files/image298.gif) ,函数f(x)在(0,+∞)上单调递增,不合题意;┉┉┉11分
,函数f(x)在(0,+∞)上单调递增,不合题意;┉┉┉11分
(本小题满分12分)已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项。
(1)求数列{an}的通项公式;
(2)若bn=![]() ,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。
,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。
(本小题满分12分)
已知单调递增的等比数 列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项。
列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项。
(1)求数列{an}的通项公式;
(2)若b n=
n= ,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。
,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。
(09年临沂一模理)(12分)
已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项。
(1)求数列{an}的通项公式;
(2)若bn=![]() ,sn=b1+b2+┉+bn,求sn+n•
,sn=b1+b2+┉+bn,求sn+n•![]() >50成立的正整数 n的最小值。
>50成立的正整数 n的最小值。
.files/image100.gif)
.files/image102.gif)
.files/image104.gif)
.files/image106.gif)
.files/image108.gif)
.files/image111.gif)
.files/image113.gif)
.files/image115.gif)
.files/image117.gif)
.files/image119.gif)
.files/image121.gif)
.files/image123.gif)
.files/image125.gif)
.files/image127.gif)
.files/image129.gif)
.files/image131.gif)
.files/image133.gif)
.files/image135.gif)
.files/image137.gif)
.files/image139.gif)
.files/image141.gif)
.files/image143.gif)
.files/image145.gif)
.files/image147.gif)
.files/image149.gif)
.files/image151.gif)
.files/image153.gif)
.files/image155.gif)
.files/image157.gif)
.files/image159.gif)
.files/image161.gif)
.files/image163.gif)
.files/image165.gif)
.files/image167.gif)
.files/image169.gif)
.files/image171.gif)
.files/image173.gif)
.files/image175.gif)
.files/image177.gif)
.files/image179.gif)
.files/image181.gif)
.files/image183.gif)
.files/image185.gif)
.files/image189.gif)
.files/image196.gif)
.files/image198.gif)
.files/image200.gif)
.files/image020.gif)
.files/image213.gif)
.files/image215.gif)
.files/image217.gif)
.files/image219.gif)
.files/image221.gif)
.files/image223.gif)
.files/image225.gif)
.files/image227.gif)
.files/image233.gif)
.files/image235.gif)
.files/image237.gif)
.files/image239.gif)
.files/image241.gif)
.files/image243.gif)
.files/image245.gif)
.files/image247.gif)
.files/image249.gif)
.files/image251.gif)
.files/image253.gif)
.files/image257.gif)
.files/image259.gif)
.files/image261.gif)
.files/image263.gif)
.files/image265.gif)
.files/image267.gif)
.files/image269.gif)
.files/image271.gif)
.files/image273.gif)
.files/image275.gif)
.files/image277.gif)
.files/image279.gif)
.files/image281.gif)
.files/image283.gif)
.files/image285.gif)
.files/image287.gif)
.files/image289.gif)
.files/image291.gif)
.files/image294.gif)
.files/image300.gif)
.files/image302.gif)
.files/image304.gif)
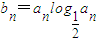 ,Sn=b1+b2+…+bn,求使Sn+n•2n+1>62成立的正整数n的最小值.
,Sn=b1+b2+…+bn,求使Sn+n•2n+1>62成立的正整数n的最小值.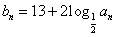 ,Sn=b1+b2+…+bn,求Sn的最大值。
,Sn=b1+b2+…+bn,求Sn的最大值。