摘要：(3)设直线AB的方程为.那么有:
网址：http://m.1010jiajiao.com/timu_id_37842[举报]
已知：在△ABC中，∠ACB=90°，AC=BC，现将一块边长足够大的直角三角板的直角顶点置于AB的中点O处，两直角边分别经过点B、C，然后将三角板绕点O按顺时针方向旋转一个角度反（0°＜a＜90°），旋转后，直角三角板的直角边分别与AC、BC相交于点K、H，四边形CHOK是旋转过程中三角板与△ABC的重叠部分（如图1所示）．那么，在上述旋转过程中：
（1）如图1，线段BH与CK具有怎样的数量关系？四边形CHOK的面积是否发生变化？请说明你发现的结论的理由．
（2）如图2，连接HK，
①若AK=12，BH=5，求△OKH的面积；
②若AC=BC=4，设BH=x，当△CKH的面积为2时，求x的值，并说出此时四边形CHOK是什么特殊四边形．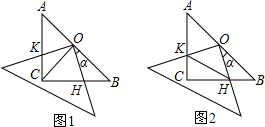
查看习题详情和答案>>
（1）如图1，线段BH与CK具有怎样的数量关系？四边形CHOK的面积是否发生变化？请说明你发现的结论的理由．
（2）如图2，连接HK，
①若AK=12，BH=5，求△OKH的面积；
②若AC=BC=4，设BH=x，当△CKH的面积为2时，求x的值，并说出此时四边形CHOK是什么特殊四边形．
查看习题详情和答案>>
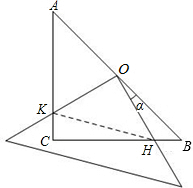在△ABC中，∠ACB=90°，AC=BC=4，现将一块边长足够大的直角三角板的直角顶点置于AB的中点O，两直角边分别经过点B、C，然后将三角板绕点O按顺时针方向旋转一个角度α（0°＜α＜90°），旋转后，直角三角板的直角边分别与AC、BC相交于点K、H，四边形CHOK是旋转过程中三角板与△ABC的重叠部分（如图所示），那么，在上述旋转过程中：（1）线段BH与CK具有怎样的数量关系？四边形CHOK的面积是否发生变化？证明你发现的结论；
（2）连接HK，设BH=x．当△CKH的面积为
| 3 | 2 |
已知：在△ABC中，∠ACB=90°，AC=BC，现将一块边长足够大的直角三角板的直角顶点置于AB的中点O处，两直角边分别经过点B、C，然后将三角板绕点O按顺时针方向旋转一个角度反（0°＜a＜90°），旋转后，直角三角板的直角边分别与AC、BC相交于点K、H，四边形CHOK是旋转过程中三角板与△ABC的重叠部分（如图1所示）．那么，在上述旋转过程中：
（1）如图1，线段BH与CK具有怎样的数量关系？四边形CHOK的面积是否发生变化？请说明你发现的结论的理由．
（2）如图2，连接HK，
①若AK=12，BH=5，求△OKH的面积；
②若AC=BC=4，设BH=x，当△CKH的面积为2时，求x的值，并说出此时四边形CHOK是什么特殊四边形．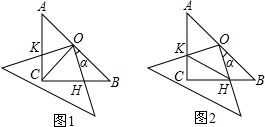
查看习题详情和答案>>
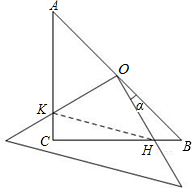在△ABC中，∠ACB=90°，AC=BC=4，现将一块边长足够大的直角三角板的直角顶点置于AB的中点O，两直角边分别经过点B、C，然后将三角板绕点O按顺时针方向旋转一个角度α（0°＜α＜90°），旋转后，直角三角板的直角边分别与AC、BC相交于点K、H，四边形CHOK是旋转过程中三角板与△ABC的重叠部分（如图所示），那么，在上述旋转过程中：
（1）线段BH与CK具有怎样的数量关系？四边形CHOK的面积是否发生变化？证明你发现的结论；
（2）连接HK，设BH=x．当△CKH的面积为
时，求出x的值．
查看习题详情和答案>>
已知：在△ABC中，∠ACB=90°，AC=BC，现将一块边长足够大的直角三角板的直角顶点置于AB的中点D处，两直角边分别经过点B、C，然后将三角板绕点D按顺时针方向旋转一个角度α（0°＜a＜90°），旋转后，直角三角板的直角边分别与AC、BC相交于点K、H，四边形CHOK是旋转过程中三角板与△ABC的重叠部分（如图1所示）．那么，在上述旋转过程中：
（1）如图1，线段BH与CK具有怎样的数量关系？四边形CHOK的面积是否发生变化？请说明你发现的结论的理由．
（2）如图2，连接HK，
①若AK=12，BH=5，求△OKH的面积；
②若AC=BC=4，设BH=x，当△CKH的面积为2时，求x的值，并说出此时四边形CHOK是什么特殊四边形．
（1）如图1，线段BH与CK具有怎样的数量关系？四边形CHOK的面积是否发生变化？请说明你发现的结论的理由．
（2）如图2，连接HK，
①若AK=12，BH=5，求△OKH的面积；
②若AC=BC=4，设BH=x，当△CKH的面积为2时，求x的值，并说出此时四边形CHOK是什么特殊四边形．
