摘要：23．15-16世纪.意大利数学家们曾讨论过“如果两人赌博提前结束.该如何分配赌金 等问题．比如.两个人做掷硬币游戏.掷得正面甲得一分.掷得反面乙得一分.先得到10分的人赢得一个大蛋糕．如果游戏因故中途结束.此时甲得8分.乙得7分.那么他们该如何分配这个蛋糕?
网址：http://m.1010jiajiao.com/timu_id_371742[举报]
10、同学们曾玩过万花筒，它是由三块等宽等长的玻璃片围成的．如图是看到的万花筒的一个图案，图中所有小三角形均是全等的等边三角形，其中的菱形AEFG可以看成是把菱形ABCD以A为中心（ ）
查看习题详情和答案>>
一位老人非常喜欢孩子，每当有孩子到他家做客时，老人都要拿出糖果招待他们．来一个孩子，老人就给孩子一块糖；来两个孩子，老人就给每个孩子两块糖…
（1）第一天有a个男孩去了老人家，老人一共给了这些孩子a2块糖；
（2）第二天有b个女孩去了老人家，老人一共给了这些孩子b2块糖；
（3）第三天这（a+b）个孩子一起去了老人家，老人一共给了这些孩子（a+b）2块糖．
这些孩子第三天得到的糖果数与前两天他们得到的糖果总数相比哪个多，哪个少？为什么？经过思考可知，a个男孩每人多得了b块糖，b个女孩每人多得了a块糖，因此多得了ab+ab=2ab块糖，即有（a+b）2=a2+b2+2ab．
我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休”．在一定条件下，数和形之间可以相互转化，相互渗透．
体会数形结合思想的内涵，试设计一种图形来说明（a+b）2=a2+b2+2ab．（要求：画出图形，并利用图形作必要的推理说明）
查看习题详情和答案>>
（1）第一天有a个男孩去了老人家，老人一共给了这些孩子a2块糖；
（2）第二天有b个女孩去了老人家，老人一共给了这些孩子b2块糖；
（3）第三天这（a+b）个孩子一起去了老人家，老人一共给了这些孩子（a+b）2块糖．
这些孩子第三天得到的糖果数与前两天他们得到的糖果总数相比哪个多，哪个少？为什么？经过思考可知，a个男孩每人多得了b块糖，b个女孩每人多得了a块糖，因此多得了ab+ab=2ab块糖，即有（a+b）2=a2+b2+2ab．
我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休”．在一定条件下，数和形之间可以相互转化，相互渗透．
体会数形结合思想的内涵，试设计一种图形来说明（a+b）2=a2+b2+2ab．（要求：画出图形，并利用图形作必要的推理说明）
同学们曾玩过万花筒，它是由三块等宽等长的玻璃片围成的，如图所示，图中所有的小三角形是全等的等边三角形，其中的菱形AEFG，可以看成是把菱形ABCD以点A为中心逆
逆
（填“顺”或“逆”）时针旋转120
120
度得到的．
6、同学们曾玩过万花筒，它是由三块等长的玻璃片围成的．如图，是在万花筒中看到的一个图案．图中所有小三角形均是全等的等边三角形，其中的菱形AEFG可以看成把菱形ABCD以A为旋转中心（ ）
查看习题详情和答案>>
我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休”．数学中，数和形是两个最主要的研究对象，它们之间有着十分密切的联系，在一定条件下，数和形之间可以相互转化，相互渗透．
数形结合的基本思想，就是在研究问题的过程中，注意把数和形结合起来考察，斟酌问题的具体情形，把图形性质的问题转化为数量关系的问题，或者把数量关系的问题转化为图形性质的问题，使复杂问题简单化，抽象问题具体化，化难为易，获得简便易行的成功方案．
例如：求1+2+3+4+…+n的值，其中n是正整数．
对于这个求和问题，如果采用纯代数的方法（首尾两头加），问题虽然可以解决，但在求和过程中，需对n的奇偶性进行讨论．
如果采用数形结合的方法，即用图形的性质来说明数量关系的事实，那就非常的直观．现利用图形的性质来求1+2+3+4+…+n的值，方案如下：如图，斜线左边的三角形图案是由上到下每层依次分别为1，2，3，…，n个小圆圈排列组成的．而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+n的值．为求式子的值，现把左边三角形倒放于斜线右边，与原三角形组成一个平行四边形．此时，组成平行四边形的小圆圈共有n行，每行有（n+1）个小圆圈，所以组成平行四边形小圆圈的总个数为n（n+1）个，因此，组成一个三角形小圆圈的个数为
，即1+2+3+4+…+n=
．
（1）仿照上述数形结合的思想方法，设计相关图形，求1+3+5+7+…+（2n-1）的值，其中n是正整数．（要求：画出图形，并利用图形做必要的推理说明）
（2）试设计另外一种图形，求1+3+5+7+…+（2n-1）的值，其中n是正整数．（要求：画出图形，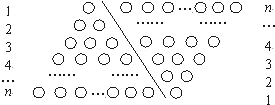
并利用图形做必要的推理说明）
查看习题详情和答案>>
数形结合的基本思想，就是在研究问题的过程中，注意把数和形结合起来考察，斟酌问题的具体情形，把图形性质的问题转化为数量关系的问题，或者把数量关系的问题转化为图形性质的问题，使复杂问题简单化，抽象问题具体化，化难为易，获得简便易行的成功方案．
例如：求1+2+3+4+…+n的值，其中n是正整数．
对于这个求和问题，如果采用纯代数的方法（首尾两头加），问题虽然可以解决，但在求和过程中，需对n的奇偶性进行讨论．
如果采用数形结合的方法，即用图形的性质来说明数量关系的事实，那就非常的直观．现利用图形的性质来求1+2+3+4+…+n的值，方案如下：如图，斜线左边的三角形图案是由上到下每层依次分别为1，2，3，…，n个小圆圈排列组成的．而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+n的值．为求式子的值，现把左边三角形倒放于斜线右边，与原三角形组成一个平行四边形．此时，组成平行四边形的小圆圈共有n行，每行有（n+1）个小圆圈，所以组成平行四边形小圆圈的总个数为n（n+1）个，因此，组成一个三角形小圆圈的个数为
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
（1）仿照上述数形结合的思想方法，设计相关图形，求1+3+5+7+…+（2n-1）的值，其中n是正整数．（要求：画出图形，并利用图形做必要的推理说明）
（2）试设计另外一种图形，求1+3+5+7+…+（2n-1）的值，其中n是正整数．（要求：画出图形，
并利用图形做必要的推理说明）
查看习题详情和答案>>