网址:http://m.1010jiajiao.com/timu_id_371203[举报]
一、选择题(每小题5分,共60分)
BDACC ACDDB AA
二、填空题(每小题4分,共16分)
(13) ; (14)
; (14) ; (15)
; (15) ; (16)②③。
; (16)②③。
三、解答题(共74分)
(17)解:(I)由于弦定理 ,
,
有
代入 得
得 。
。
…………………………………4分
即 。
。
 ……………………………………6分
……………………………………6分

 ……………………………………7分
……………………………………7分
 …………………………………8分
…………………………………8分
(Ⅱ) ,
………………………………10分
,
………………………………10分
由 ,得
,得 。
………………………………11分
。
………………………………11分
所以,当 时,
时, 取得最小值为0, ………………………………12分
取得最小值为0, ………………………………12分
(18)解:(I)由已知得
故
即
故数列 为等比数列,且
为等比数列,且
又当 时,
时,
 ………………………………6分
………………………………6分
而 亦适合上式
亦适合上式
 …………………………………8分
…………………………………8分
(Ⅱ)
所以

 ………………………………12分
………………………………12分
(19)解:(I)由该四棱锥的三视图可知,该四棱锥 的底面的边长为1的正方形,侧棱
的底面的边长为1的正方形,侧棱 ,
,
……………………………4分
 (Ⅱ)连结
(Ⅱ)连结 交
交 于
于 ,则
,则 为
为 的中点,
的中点,
 为
为 的中点,
的中点,
 ,
,
又 平面
平面 内,
内,
 平面
平面 ………………8分
………………8分
(Ⅲ)不论点 在何位置,都有
在何位置,都有 ………………9分
………………9分
证明:连结 ,
, 是正方形,
是正方形,



又 ,
,

 …………12分
…………12分
(20分)解:
(I)利用树形图我们可以列出连续抽取2张卡片的所有可能结果(如下图所示)。

由上图可以看出,实验的所有可能结果数为20.因为每次都随机抽取,因次
这20种结果出现的可能性是相同的,实验属于古典概型。 ……………2分用
 表示事“连续抽取2人都是女生”,则
表示事“连续抽取2人都是女生”,则 与
与 互斥,并且
互斥,并且 表示事
表示事
件“连续抽取2张卡片,取出的2人不全是男生”,由列出的所有可能结果可
以看出, 的结果有12种,
的结果有12种, 的结果有2种,由互斥事件的概率加法公式,
的结果有2种,由互斥事件的概率加法公式,
可得
 ,
,
即连续抽取2张卡片,取出的2人不全是男生的概率为0.7……………6分
(Ⅱ)有放回地连续抽取2张卡片,需注意同一张卡片可再次被取出,并且它被取出的可能性和其他卡片相等,我们用一个有序实数对表示抽取的结果,例如“第一次取出2号,第二次取出4号”就用(2,4)来表示,所有的可能结果可以用下表列出。
 第二次抽取
第二次抽取
第一次抽取
1
2
3
4
5
1
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
2
(2,1)
(2,2)
(2,3)
(2,4)
(2,5)
3
(3,1)
(3,2)
(3,3)
(3,4)
(3,5)
4
(4,1)
(4,2)
(4,3)
(4,4)
(4,5)
5
(5,1)
(5,2)
(5,3)
(5,4)
(5,5)
试验的所有可能结果数为25,并且这25种结果出现的可能性是相同的,试验属于古典型。 …………………………8分
用 表示事件“独唱和朗诵由同一个人表演”,由上表可以看出,
表示事件“独唱和朗诵由同一个人表演”,由上表可以看出, 的结果共
的结果共
有5种,因此独唱和朗诵由同一个人表演的概率
 ……………………………12分
……………………………12分
(21)解:
(I)
依题意有 ………………………2分
………………………2分
即 解得
解得 …………………………4分
…………………………4分

由 ,得
,得
 的单调递减区间是
的单调递减区间是 ………………………6分
………………………6分
(Ⅱ)由 得
得 ………………………8分
………………………8分
不等式组确定的平面区域如图阴影部分所示:
由 得
得 ………………………8分
………………………8分
 不等式组确定的平面区域如图阴影部分所示:
不等式组确定的平面区域如图阴影部分所示:
由 得
得
 点的坐标为(0,-1). ………………10分
点的坐标为(0,-1). ………………10分
设 则
则 表示平面区域内的点(
表示平面区域内的点( )与点
)与点
 连线斜率。
连线斜率。
 由图可知
由图可知 或
或 ,
,
即 ……………12分
……………12分
(22)解:
(I)设椭圆方程为
则根据题意,双曲线的方程为
 且满足
且满足
 解方程组得
解方程组得 ……………………4分
……………………4分
 椭圆的方程为
椭圆的方程为 ,双曲线的方程
,双曲线的方程 ………………6分
………………6分
(Ⅱ)由(I)得
设 则由
则由 得
得 为
为 的中点,所以
的中点,所以 点坐标为
点坐标为
 ,
,
将 坐标代入椭圆和双曲线方程,得
坐标代入椭圆和双曲线方程,得

消去 ,得
,得
解之得 或
或 (舍)
(舍)
所以 ,由此可得
,由此可得
所以 …………………………10分
…………………………10分
当 为
为 时,直线
时,直线 的方程是
的方程是
即
代入 ,得
,得
所以 或-5(舍)
……………………………12分
或-5(舍)
……………………………12分
所以
 轴。
轴。
所以 ……………………14分
……………………14分
给出下列四个命题:
①命题“![]() ”的否定是“
”的否定是“![]() ”;
”;
②线性相关系数r的绝对值越接近于1,表明两个随机变量线性相关性越强;
③若a,b![]()
④函数![]() 在
在![]() 上恒为正,则实数a的取值范围是
上恒为正,则实数a的取值范围是![]()
其中真命题的序号是 。(请填上所有真命题的序号)
查看习题详情和答案>>给出下列四个命题:
①命题“![]() ”的否定是“
”的否定是“![]() ”;
”;
②线性相关系数r的绝对值越接近于1,表明两个随机变量线性相关性越强;
③若a,b![]()
④函数![]() 在
在![]() 上恒为正,则实数a的取值范围是
上恒为正,则实数a的取值范围是![]()
其中真命题的序号是 。(请填上所有真命题的序号)
查看习题详情和答案>>给出下列四个命题:
①函数f(x)=lnx-2+x在区间(1 , e)上存在零点;
②若m≥-1,则函数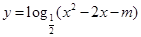 的值域为R;
的值域为R;
③若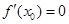 ,则函数y=f(x)在x=x0处取得极值;
,则函数y=f(x)在x=x0处取得极值;
④“a =1”是“函数 在定义域上是奇函数”的充分不必要条件。
在定义域上是奇函数”的充分不必要条件。
其中正确的是 。
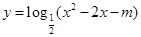 的值域为R;
的值域为R;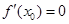 ,则函数y=f(x)在x=x0处取得极值;
,则函数y=f(x)在x=x0处取得极值; 在定义域上是奇函数”的充分不必要条件。
在定义域上是奇函数”的充分不必要条件。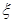 ~
~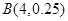 ,则
,则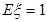
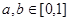 ,则不等式
,则不等式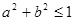 成立的概率是
成立的概率是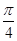 ;
; 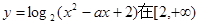 上恒为正,则实数a的取值范围是
上恒为正,则实数a的取值范围是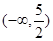 。
。